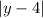Question

Refer to your answers to the questions from Part 1 of Project 1.

Any point on the parabola can be labeled (x,y) as shown.
What are the distances from the point (x,y) to the focus of the parabola and the directrix? SELECT TWO ANSWERS.

Answer 1

`\textsf{Distance\;to\;the\;focus:\;$√((x+3)^2+(y-2)^2)$}`

`\textsfDistance\;to\;the\;directrix:\;$`

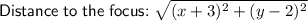
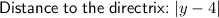
Explanation:

Distance to the focus

The focus of a parabola is a fixed point on the axis of symmetry. It is located inside the parabola and is equidistant from all points on the parabola. Therefore, the focus of the given parabola is (-3, 2).

To find the distance from a point (x, y) to the focus of the parabola, we can use the distance formula

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

where (x₁, y₁) and (x₂, y₂) are the two points.

Let (x₁, y₁) = (-3, 2)

Let (x₂, y₂) = (x, y)

Substitute the points into the distance formula:

`d=√((x-(-3))^2+(y-2)^2)`

`d=√((x+3)^2+(y-2)^2)`

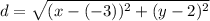
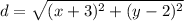
Therefore, the distance to the focus is:

`√((x+3)^2+(y-2)^2)`

`\hrulefill`

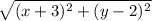
Distance to the directrix

The directrix of a parabola is a fixed line positioned outside the parabola, and perpendicular to the axis of symmetry. Therefore, the directrix of the given parabola is y = 4.

The distance from any point on the parabola to the directrix is the absolute value of the difference between the y-coordinate of the point and the y-coordinate of the directrix. Therefore:

`d = |y - 4|`

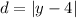
Therefore, the distance to the directrix is:

`|y-4|`