Question

The picture pls help

Answer 1

x ≈ 1.2.

Explanation:

In order to solve the equation using a graphing calculator, we can plot the two functions involved and find their intersection points.

First, we define the two functions:

• Function 1:
  `\tt f(x) = 3\log_2(x)`
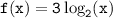
• Function 2:
  `\tt g(x) = x^3 - 4x^2 + 4x`

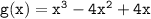
Next, we plot these functions on the graphing calculator.

We can do this by entering the equations for the functions into the calculator and setting the viewing window to see a range of x-values that includes x = 3.3 and the potential intersection points.

Once the graph is plotted, we can locate the point of intersection between the two curves.

The x-coordinate of this point represents the other solution to the equation, as we already know one solution is x = 3.3.

We can read the corresponding x-value from the graphing calculator to find the other solution.

In this case, the graph of the two functions intersects at two points: (3.3, 5.1) and (1.2, 0.8).

Therefore, the two solutions to the equation are x = 3.3 and x = 1.8.

Answer 2

x ≈ 1.2

Explanation:

Given equation:

`3 \log_2(x)=x^3-4x^2+4x`

Rewrite the equation in the form f(x) = g(x). Therefore:

`f(x)=3\log_2(x)`

`g(x)=x^3-4x^2+4x`

By graphing the functions and identifying the points of intersection, we can determine the approximate values of x that satisfy the equation.

Plot the graphs of f(x) and g(x) using a graphing calculator (see attached).

Find the x-values of the points where the two graphs intersect. These x-values are the solutions to the equation.

`x = 3.25277034... \approx 3.3`

`x = 1.195685730... \approx 1.2`

Therefore, the solution other than x ≈ 3.3 is x ≈ 1.2.