Question

!50 POINTS! (2 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1. A, C, D area parallelograms
2. x = 75°

Explanation:

For the given geometries, you want to identify the parallelograms, and the value of the angle marked x.

1. Parallelograms

The four illustrations show the various properties of a parallelogram:

(a) opposite angles are congruent

(b) opposite sides are parallel (both pairs); opposite sides are the same length (both pairs)

(c) the diagonals bisect each other

(d) adjacent angles are supplementary (see also (a))

Note that one pair of opposite sides parallel and one pair of opposite sides the same length (figure (b)) is not sufficient to restrict the figure to being a parallelogram. This is illustrated in the attachment, which shows an isosceles trapezoid with one pair of parallel sides and one pair of congruent sides.

The parallelograms are A, C, D.

2. Angle x

In this isosceles trapezoid, angle E (aka x) is congruent to angle C and supplementary to angle B.

x = 180° -105°

x = 75°

Answer 2

1st question:

• three options: a, b, and d.

2nd question:

• x = 52.5

Explanation:

Gor 1st Question:

Properties of Parallelogram:

• Opposite sides are parallel and equal

• Opposite angles are equal

• Adjacent angles are supplementary

• Diagonals bisect each other

a.

a is parallelogram because the opposite angles are equal.

b.

b is parallelogram because opposite sides are parallel and equal

c.

c is not a parallelogram because its diagonals bisect each other but the opposite side are not parallel.

d.

d is a parallelogram cause opposite angles are equal.

Therefore, three options are a, b, and d.

`\hrulefill`

For 2nd question:

Given:

ABCD is a parallelogram.

m∡B=105°

ED ≅ AD

To find:

x=?

Solution:

m∡B = m∡ADC since the sum of the opposite angle of a parallelogram is equal.

m∡ADC=105°

Again,

if two sides are equal, then it is an isoceles triangle

m∡A=m∡E =x since the base angle of an isoceles triangle

Again,

m∡A+m∡E=m∡ADC since exterior angle of the triangle is equal to the sum of two opposite interior angle

x+x=105°

2x=105°

x=
`\tt (105)/(2)`

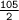
x=52.5

Therefore, value of x is 52.5.