Question

The equation of the hyperbola that has a center at (3, 4), a focus at (-2, 4), and a vertex at (6,4), is

(x-C)^2/A^2 - (y-D)^2/B^2 =1

where
A =
B=
C=
D=

Answer 1

A = 3

B = 4

C = 3

D = 4

Explanation:

The distance between the focus and the center of the hyperbola is 5 units, so following the equation
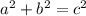`a^2+b^2=c^2` where
`a=3` is the distance between the center and vertex, we can determine the value of
`b`:

`a^2+b^2=c^2\\3^2+b^2=5^2\\9+b^2=25\\b^2=16\\b=4`

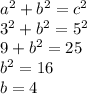
Also, since the center is
`(3,4)`, then C and D are 3 and 4 respectively.