Answer:
1st question:
- All of the sides are congruent.
- The diagonals are perpendicular
- The diagonals bisect opposite angles.
2nd Question:
3rd Question:
Explanation:
The three properties that are true for a square but not for all rectangles:
- All of the sides are congruent.
- This is not true for all rectangles, as a rectangle can have two pairs of equal sides, but the two pairs of sides can be different lengths.
- The diagonals bisect each other at right angles.
- This is not true for all rectangles, as the diagonals of a rectangle can bisect each other at an angle other than 90 degrees.
- The diagonals bisect opposite angles.
- The diagonals of a rectangle do not necessarily bisect opposite angles. However, the diagonals of a square do bisect opposite angles.
All other properties are true for both square and rectangle.

For 2nd Question:
Given:
m∡IEF=36°
EFGH is a isosceles triangle
EFGI is Parallelogram
It means
IG║EF and GF║IE
To find:
m ∡HGI=?
Solution:
m∡IEF=m∡HIG Being the corresponding angle
m∡HIG = 36°
again,
m∡IEF= m∡IGF since the opposite angle of a parallelogram is equal.
m∡IGF = 36°
again,
m∡IEF = m∡GHI
m∡GHI = 36°
Since the triangle of two sides of an isosceles trapezoid are congruent and their respective angle is also congruent.
Now,
In Δ GHI
m∡GHI + m∡HIG + m∡HGi =180°
SInce the sum of the interior angle of the triangle is supplementary.
36°+36°+ m∡HGi =180°
m∡HGi =180°-36°-36°
therefore, m∡HGI=108°

For 3rd Question:
Given:
m∡A=100°
m∡B=13x
m∡C=7x+y
ABCD is a parallelogram.
it means: AD ║ BC and AB║CD
To find.
y=?
Solution:
∡A+∡B =180° Being co interior angle
100°+ 13x=180°
13x=180°-100°
13x=80°
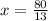
x=6.154
again,
∡A=∡C since the corresponding angle of the parallelogram is equal.
100°=7x+y
100°=7*6.15+y
y=100°-7*6.154
y=56.92
Therefore, the value of y is 56.92