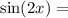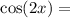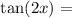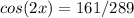
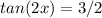
For the first problem, its given that
 and
and
 is in Quadrant I. To find
is in Quadrant I. To find
 , we'll use the double-angle identity for tangent:
, we'll use the double-angle identity for tangent:
![\[\tan(2\theta) = (2\tan(\theta))/(1 - \tan^2(\theta))\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/sg9ay6eb73qmv9cx4v648yoy2tr5192mtw.png)
Given that
 and
and
 is in Quadrant I,
is in Quadrant I,
 can be found using the Pythagorean identity:
can be found using the Pythagorean identity:
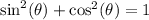 .
.
![\[\sin(\theta) = √(1 - \cos^2(\theta)) = \sqrt{1 - \left((3)/(5)\right)^2} = (4)/(5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4lllygt57j31m0jmak3auq3lpl89hlq5cq.png)
Now,
 .
.
So, using the double-angle formula for tangent:
![\[\tan(2\theta) = (2\tan(\theta))/(1 - \tan^2(\theta)) = (2 \cdot (4)/(3))/(1 - \left((4)/(3)\right)^2) = (8/3)/(1 - 16/9) = (8/3)/(-7/9) = -(24)/(7)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ps48drmf8xkrbf0k6cui0jqx9w5xxcdpwj.png)
For the second problem, its given
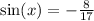 and
and
 is in Quadrant III. To find
is in Quadrant III. To find
 ,
,
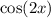 , and
, and
 , we'll use the double-angle identities.
, we'll use the double-angle identities.
Given that
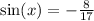 and
and
 is in Quadrant III, we can use the Pythagorean identity to find
is in Quadrant III, we can use the Pythagorean identity to find
 :
:
![\[\cos(x) = -√(1 - \sin^2(x)) = -\sqrt{1 - \left(-(8)/(17)\right)^2} = -\sqrt{1 - (64)/(289)} = -\sqrt{(225)/(289)} = -(15)/(17)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/idita7h3v7jbbxzvsywo49vvxpts3xw1sx.png)
Now, using the double-angle identities:
![\[\sin(2x) = 2\sin(x)\cos(x) = 2 \cdot \left(-(8)/(17)\right) \cdot \left(-(15)/(17)\right) = (240)/(289)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/jdx2g4wcifd25r1ovf9y1ec3u0hbcutia5.png)
![\[\cos(2x) = \cos^2(x) - \sin^2(x) = \left(-(15)/(17)\right)^2 - \left(-(8)/(17)\right)^2 = (225)/(289) - (64)/(289) = (161)/(289)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/7otpkq94vfgs9gkmitz6lqnr2ew11w99ho.png)
![\[\tan(2x) = (\sin(2x))/(\cos(2x)) = ((240)/(289))/((161)/(289)) = (240)/(161) = (120)/(80) = (3)/(2)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xh5l5bh984h08ksxu6ct88onawiqznm03h.png)
The complete question is here:
Evaluate the expression under the given conditions.
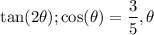 in Quadrant I
in Quadrant I
Find
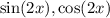 and
and
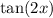 from the given information.
from the given information.
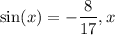 in Quadrant III
in Quadrant III