a. The average power required for the chair-lift is approximately 3428.5 watts or 3.43 kilowatts.
b. The required capacity of the motor, considering the
 overload, is approximately 21.05 kilowatts.
overload, is approximately 21.05 kilowatts.
To determine the average power required for the chair-lift, we can use the formula for power:
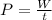
Where:
-
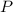 is the power (in watts, W)
is the power (in watts, W)
-
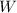 is the work done (in joules, J)
is the work done (in joules, J)
-
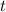 is the time (in seconds, s)
is the time (in seconds, s)
First, let's calculate the work done to transport 1000 skiers from the base A to the summit B, which is a vertical distance of 750 meters. We'll also account for the
 overload, which means we need to calculate the work for transporting
overload, which means we need to calculate the work for transporting
 more skiers in the same time.
more skiers in the same time.
(a) Work Done:
The work done to lift a mass against gravity is given by the formula:
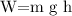
Where:
-
 is the mass (in kg)
is the mass (in kg)
-
 is the acceleration due to gravity (approximately
is the acceleration due to gravity (approximately
 )
)
-
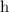 is the height (in meters)
is the height (in meters)
Let's calculate the work done for one skier:
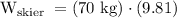
Now, we need to account for the $300 \%$ overload, so the total work done for 1000 skiers is:

Now, we'll calculate the time it takes to transport the skiers at a speed of
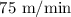 :
:
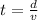
Where:
-
 is the distance
is the distance
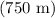
-
 is the speed
is the speed

Convert the speed to meters per second:
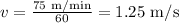
Now, calculate the time:

Now, we can calculate the average power required:

So, the average power required for the chair-lift is approximately 3428.5 watts or 3.43 kilowatts.
(b) Required Capacity of the Motor:
The mechanical efficiency is given as
 . Mechanical efficiency is defined as the ratio of useful work output to the total work input. So, we can write:
. Mechanical efficiency is defined as the ratio of useful work output to the total work input. So, we can write:
Efficiency = Useful Work Output/Total Work Input
We can rearrange this equation to find the total work input:
Total Work Input = Useful Work Output / Efficiency
In this case, the useful work output is the work done to transport the skiers, which is
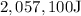 , and the efficiency is
, and the efficiency is
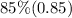 .
.
Total Work Input
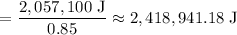
Now, we need to account for the
 overload, so the total work input for the motor is: Total Work Input
overload, so the total work input for the motor is: Total Work Input
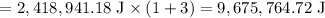
The motor has to do this amount of work in 600 seconds (the time it takes to transport the skiers):
Power Required = Total Work Input,
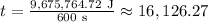 watts
watts
To account for the overload, the motor should have a capacity that can handle this power, so we'll consider the power with the overload:
Required Motor Capacity:

So, the required capacity of the motor, considering the
 overload, is approximately 21.05 kilowatts.
overload, is approximately 21.05 kilowatts.