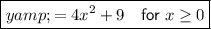Question

Find a direct relationship between y and x.
x = √3t and y = 12t + 9

for x ≥ 0

Answer 1

`y=4x^2+9`

Explanation:

Given parametric equations:

`x=√(3t),\qquad x \geq 0`

`y=12t+9`

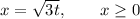
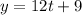
To find a direct relationship between y and x, begin by rearranging the first equation to isolate t:

`\begin{aligned} x&=√(3t)\\\\x^2&=(√(3t))^2\\\\x^2&=3t\\\\(x^2)/(3)&=(3t)/(3)\\\\t&=(x^2)/(3)\end{aligned}`

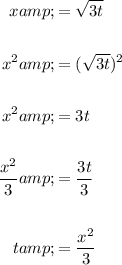
Substitute the found expression for t into the equation for y:

`\begin{aligned}t=(x^2)/(3) \implies y&=12\left((x^2)/(3)\right)+9\\\\y&=4x^2+9\end{aligned}`

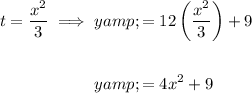
Therefore, the direct relationship between y and x is:

`\boxed{y&=4x^2+9 \quad \textsf{for}\;x \geq 0}`