Question

what is the value of $x$ if a cube's volume is $5x$ cubic units and its surface area is $x$ square units?

Answer 1

The value of $x$ is determined by using the formulas for the volume and surface area of a cube. After setting the equations based on the given values and solving for $x$, we conclude that the only logical solution is that the value of $x$ must be zero.

Step-by-step explanation:

The student has asked what the value of $x$ is if a cube's volume is $5x$ cubic units and its surface area is $x$ square units. To find the value of $x$, we can first express the volume and surface area of a cube using its side length $s$.

The formulas are volume = $s^3$ and surface area = $6s^2$ respectively. Since the cube's volume is $5x$ and its surface area is $x$, we can set up the equations $s^3 = 5x$ and $6s^2 = x$.

We then solve for $s$ in the surface area equation, which gives us $s^2 = x/6$, and then take the cube root of both sides to get $s = (x/6)^(1/2)$. Substituting this value into the volume equation $s^3 = 5x$, we can find the value of $x$.

By solving $((x/6)^(1/2))^3 = 5x$, we get $x/6 = 5x$, which simplifies to $x = 30x$. This means $x$ equals zero. Therefore, the value of $x$ is zero.

Answer 2

The value of x is 900 cubic units, representing the volume of the cube.

The formula for the volume of a cube is
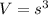`\(V = s^3\)`, where s is the length of one side of the cube.

Given that the volume of the cube is 5x cubic units, we can set up an equation:

`\[5x = s^3\]`

And the formula for the surface area of a cube is
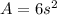`\(A = 6s^2\)`, where A is the surface area.

Given that the surface area of the cube is x square units, we can set up another equation:

`\[x = 6s^2\]`

We have a system of equations:

`\[5x = s^3\]`

`\[x = 6s^2\]`

We can solve for s using the second equation in terms of x:

`\[s^2 = (x)/(6)\]`

Now substitute this into the first equation:

`\[5x = s^3 = \left(\sqrt{(x)/(6)}\right)^3\]`

`\[5x = (x√(x))/(6)\]`

`\[30x = x√(x)\]`

`\[30 = √(x)\]`

`\[x = 30^2\]`

x = 900

Therefore, the value of x is 900 units.

Question:

What is the value of x if a cube's volume is 5x cubic units and its surface area is x square units?