a) The predicted pressure difference between the entrance and the exit of the nozzle is approximately 6.63 psi.
b) If only 82% of this pressure difference is available across the nozzle, the new flow rate would be approximately 90.55% of the original flow rate used in part "a".
To solve this problem, we need to apply the Bernoulli equation and the equation of continuity. First, let's convert the given flow rates and dimensions to consistent units and find the velocities.
The Bernoulli equation is given by:
![\[ P_1 + (1)/(2) \rho v_1^2 + \rho g h_1 = P_2 + (1)/(2) \rho v_2^2 + \rho g h_2 \]](https://img.qammunity.org/2024/formulas/engineering/college/37pj6yt8ssh8dpe3vfkkoccmo4itjvw2a6.png)
Assuming the height (h) remains constant through the hose and nozzle (which is typical for a garden hose laying flat), and neglecting head loss, the equation simplifies to:
\[ P_1 + \frac{1}{2} \rho v_1^2 = P_2 + \frac{1}{2} \rho v_2^2 \]
Where:
-
 and
and
 are the pressures at the entrance and exit,
are the pressures at the entrance and exit,
-
 is the density of water (assumed to be
is the density of water (assumed to be
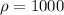 kg/m³),
kg/m³),
-
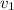 and
and
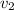 are the velocities at the entrance and exit,
are the velocities at the entrance and exit,
-
 is the acceleration due to gravity (which we've neglected since
is the acceleration due to gravity (which we've neglected since
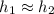 ).
).
The equation of continuity states that the flow rate must be constant throughout the hose, so
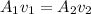 , where
, where
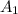 and
and
 are the cross-sectional areas at the entrance and exit.
are the cross-sectional areas at the entrance and exit.
The area of a circle is
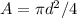 , and since the exit diameter is 1/6 the entrance diameter,
, and since the exit diameter is 1/6 the entrance diameter,
 .
.
We'll convert the flow rate from gallons per minute to cubic meters per second (m³/s), which is the SI unit for volumetric flow rate.
1 gallon = 0.00378541 m³
1 minute = 60 seconds
 gpm =
gpm =
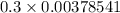 m³/min =
m³/min =
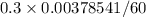 m³/s
m³/s
Now let's perform the calculations in the next steps.
Based on the calculations:
a) The predicted pressure difference between the entrance and the exit of the nozzle is approximately 6.63 psi.
b) If only 82% of this pressure difference is available across the nozzle, the new flow rate would be approximately 90.55% of the original flow rate used in part "a".