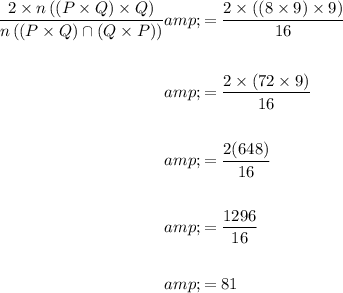Answer:
(c) 81
Explanation:
Given sets:
- P = {1, 3, 4, 5, 7, 9, 10, 12)
- Q = {2, 4, 5, 6, 9, 11, 12, 14, 15}
For two sets Q and P, the Cartesian product Q × P is defined as:
Q × P = q ∈ Q and p ∈ P
Therefore, the Cartesian product of two sets Q and P includes all possible combinations of elements from Q and P as ordered pairs. The first element in each pair comes from set Q, and the second element comes from set P.
The symbol "n" before a set represents the number of elements in that set.
Therefore, n(P × Q) represents the number of elements in the Cartesian product of sets P and Q.
There are 8 elements in set P and 9 elements in set Q. Therefore:
n(P × Q) = 8 × 9 = 72
Similarly:
n((P × Q) × Q) = (8 × 9) × 9 = 72 × 9 = 648
In the given sets P and Q, the elements 4, 5, 9, and 12 are common to both sets. After finding the Cartesian product of P × Q, as well as Q × P, the common elements in the intersection are:
((P × Q) ∩ (Q × P)) = {(4, 4), (4, 5), (4, 9), (4, 12), (5, 4), (5, 5), (5, 9), (5, 12), (9, 4), (9, 5), (9, 9), (9, 12), (12, 4), (12, 5), (12, 9), (12, 12)}
Therefore, the number of elements in ((P × Q) ∩ (Q × P)) is 16.
Therefore: