Question

Give inequalities for r and theta which describe the region below in polar coordinates. (Click on the graph for a larger version.) The two arcs shown are circular, and the region is between the two arcs and between the y-axis and line graphed, which is y = 3x. r theta (Write infinity to indicate a boundary at infinity.) Answer(s) submitted: (incorrect)

Answer 1

The region in polar coordinates is described by the inequalities
`\( (3)/(√(10)) \leq r \leq 3\sec(\theta) \) and \( (\pi)/(4) \leq \theta \leq (3\pi)/(4) \).`

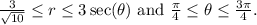
Step-by-step explanation:

To find the inequalities for ( r ) and
`\( \theta \)` that define the given region, we first need to consider the equations of the curves involved. The line ( y = 3x ) in polar coordinates corresponds to
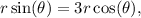`\( r\sin(\theta) = 3r\cos(\theta) \),`which simplifies to
`\( r = (3)/(\sin(\theta) - 3\cos(\theta)) \).`

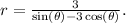
The two circular arcs form the boundaries of the region. Since the region is between the y-axis and the line ( y = 3x ), we consider the angle
`\( \theta \)`ranging from
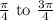`\( (\pi)/(4) \) to \( (3\pi)/(4) \)`. The outer boundary of the region is given by the equation
`\( r = 3\sec(\theta) \)`, which ensures that the region extends to infinity.

Combining these conditions, we obtain the final inequalities
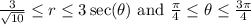`\( (3)/(√(10)) \leq r \leq 3\sec(\theta) \) and \( (\pi)/(4) \leq \theta \leq (3\pi)/(4) \)` to describe the region in polar coordinates. The lower limit for ( r ) ensures that the region is bounded by the line ( y = 3x ), and the upper limit ensures that it extends to infinity along the circular arcs. The specified range for
`\( \theta \)` ensures that the region is between the y-axis and the line ( y = 3x ).