Question

Determine the perimeter of the right triangle shown (-4,7), (-4,-1), (2,-1)

Answer 1

24 units

Explanation:

The perimeter of a two-dimensional shape is the distance all the way around the outside. Therefore, the perimeter of a triangle is the sum of its side lengths.

Let the vertices of the triangle be:

• A = (-4, 7)
• B = (-4, -1)
• C = (2, -1)

As the x-coordinates of vertices A and B are the same, the length of side AB is the difference between their y-coordinates:

`AB = 7 - (-1) = 8 \sf \; units`

As the y-coordinates of vertices B and C are the same, the length of side BC is the difference between their x-coordinates:

`BC = 2 - (-4) = 6 \sf \;units`

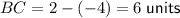
Since the x-coordinates of vertices A and B are the same, and the y-coordinates of vertices B and C are the same, sides AB and BC are the legs of the right triangle ABC. Therefore, side AC is the hypotenuse of the right triangle.

To find the length of AC, use Pythagoras Theorem:

`AB^2+BC^2=AC^2`

`8^2+6^2=AC^2`

`48+36=AC^2`

`100=AC^2`

`AC^2=100`

`√(AC^2)=√(100)`

`AC=10`

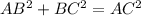
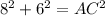
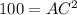
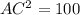
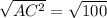
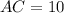
Therefore, the length of side AC is 10 units.

Finally, to determine the perimeter, sum the side lengths:

`\begin{aligned}\sf Perimeter&=AB+BC+AC\\&=8+6+10\\&=14+10\\&=24\; \sf units\end{aligned}`

Therefore, the perimeter of the right triangle with vertices at (-4, 7), (-4, -1), and (2, -1) is 24 units.