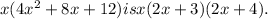The expression
 is not completely factored. To factor it further, we can use the distributive property. Let's start by factoring out the common factor x from the expression. When we do this, we get x times
is not completely factored. To factor it further, we can use the distributive property. Let's start by factoring out the common factor x from the expression. When we do this, we get x times
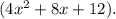
Now, let's look at the expression inside the parentheses, which is
 To factor this trinomial, we can look for two numbers whose product is equal to the product of the first and last term
To factor this trinomial, we can look for two numbers whose product is equal to the product of the first and last term
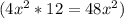 and whose sum is equal to the coefficient of the middle term (8x).
and whose sum is equal to the coefficient of the middle term (8x).
In this case, the numbers we're looking for are 6 and 8 because 6 * 8 = 48 and 6 + 8 = 14. So, we can rewrite the expression as
 .Next, we can factor by grouping. We group the first two terms (4x^2 and 6x) together and the last two terms (8x and 12) together.
.Next, we can factor by grouping. We group the first two terms (4x^2 and 6x) together and the last two terms (8x and 12) together.
Taking out the common factor from the first group gives us
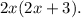 Taking out the common factor from the second group gives us
Taking out the common factor from the second group gives us
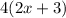 . Now, we can see that we have a common binomial factor of (2x + 3) in both terms. Finally, we can rewrite the expression as
. Now, we can see that we have a common binomial factor of (2x + 3) in both terms. Finally, we can rewrite the expression as
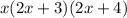 .In conclusion, the completely factored form of
.In conclusion, the completely factored form of