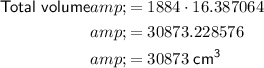Question

Volume of composite shapes.

Answer 1

1,884in³

Given

• An object made up of two cylinders.

Let the cylinder below be A & cylinder above it be B.

• Height of cylinder A = 4in
• Radius of cylinder A = 14/2in = 7in
• Height of cylinder B = 12in
• Radius of cylinder B = 12/2in = 6in
• π = 3

we know that,

• Volume of a cylinder = πr²h
• Volume of the given cylinder = Volume of cylinder A + volume of cylinder B
• => [ 3 x (7in)² x 4in ] + [ 3 x (6in)² x 12in ]
• => [ 3 x 49in² x 4in ] + [ 3 x 36in² x 12in ]
• => 588in³ + 1,296in³
• => 1,884in³

Answer 2

1884 in³

30873 cm³

Explanation:

The given object is made up of two cylinders. Therefore, to find the volume of the object, calculate the volume of each cylinder and add them together.

The formula for the volume of a cylinder is:

`\boxed{V=\pi r^2 h}`

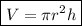
where:

• r is the radius of the circular base.
• h is the height of the cylinder.

Top cylinder

The diameter of a circle is twice its radius. Therefore, the radius of the base is 6 in, so r = 6. The height of the cylinder is 12 in, so h = 12. The given value of pi is π = 3. Therefore, the volume of the top cylinder is:

`\begin{aligned}V&=3 \cdot 6^2 \cdot 12\\&=3 \cdot 36 \cdot 12\\&=108 \cdot 12\\&=1296\; \sf in^3\end{aligned}`

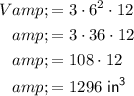
Bottom cylinder

The diameter of a circle is twice its radius. Therefore, the radius of the base is 7 in, so r = 7. The height of the cylinder is 4 in, so h = 4. The given value of pi is π = 3. Therefore, the volume of the bottom cylinder is:

`\begin{aligned}V&=3 \cdot 7^2 \cdot 4\\&=3 \cdot 49 \cdot 4\\&=147\cdot 4\\&=588\; \sf in^3\end{aligned}`

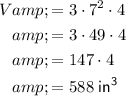
Total volume

The total volume of the composite object is the sum of the volume of the two cylinders.

`\begin{aligned}\textsf{Total volume}&=1296+588\\&=1884\; \sf in^3\end{aligned}`

Therefore, the volume of the object in cubic inches is 1884 in³.

To convert cubic inches to cubic centimeters, multiply the volume in cubic inches by 16.387064.

Therefore, the volume of the composite object in cubic centimeters is:

`\begin{aligned}\textsf{Total volume}&=1884 \cdot 16.387064\\&=30873.228576\\&=30873\; \sf cm^3\end{aligned}`