Question

There are 6 boys and 6 girls in the finals of a talent contest. A contest is held to pick the top 3 winners in both the boy and girl groups in order of talent. How many different options for winners are there?

Answer 1

14,400 different options

Explanation:

The formula for permutations is:

`\boxed{\boxed{\tt ^nP_r = (n! )/((n - r)!)}}`

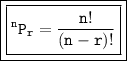
where,

• n is the number of elements in the set
• r is the number of elements to be chosen.

In this case, we need to choose 3 winners from a set of 6 boys, so we have:

• n=6
• r=3

`\tt ^6P_3 = (6! )/((6 - 3)! )= 6 * 5 * 4 = 120`

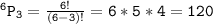
We also need to choose 3 winners from a set of 6 girls, so we have:

• n=6
• r=3

`\tt ^6P_3 = (6! )/((6 - 3)! )= 6 * 5 * 4 = 120`

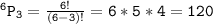
Since the order of the winners matters,

we need to multiply these two values to get the total number of possible options:

120 * 120 = 14,400

Therefore, there are 14,400 different options for winners.