Question

Find the minimum and maximum values of z=6x+3y, if possible, for the following set of constraints. 5x+8y≥40x+8y≥16x≥0,y≥0​ Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The minimum value is (Round to the nearest tenth as needed.) B. There is no minimum value. Select the correct choice below and, if necessary, fill in the answer box to complete your choice. A. The maximum value is (Round to the nearest tenth as needed.) B. There is no maximum value.

Answer 1

A. The minimum value is 0.0

B. There is no maximum value.

Step-by-step explanation:

The given problem involves optimizing the linear function \( z = 6x + 3y \) subject to a set of linear inequalities:
`\( 5x + 8y \geq 40 \), \( 4x + 8y \geq 16 \), \( x \geq 0 \), and \( y \geq 0 \)`.

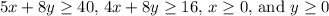To find the minimum value, we need to identify the feasible region, which is the intersection of the shaded regions defined by the inequalities.

Solving the system of inequalities, we find that the feasible region is unbounded, extending infinitely in the positive x-direction. In this region, the function \( z = 6x + 3y \) can take on values as low as 0, which occurs when both \( x \) and \( y \) are 0.

Regarding the maximum value, there is no upper bound for the feasible region. As \( x \) increases without limit, \( z \) will also increase without bound. Therefore, there is no maximum value for \( z \) within the given constraints.

In summary, the minimum value of \( z \) is 0, and there is no maximum value within the specified constraints. The absence of an upper bound on \( z \) is due to the unbounded nature of the feasible region in the positive x-direction.