Question

Harrington is a large city with a population of about 350,000 . A recently taken census found that the annual growth rate of the city is 6%. If it continues to grow at this rate how many years will it take for the population to triple in size?

Answer 1

After performing the calculation, we find that
`\( t \)` is approximately 18.85 years. Therefore, it will take nearly 18.85 years for the population to triple in size if it continues to grow at an annual rate of 6%. This is a slightly more precise calculation compared to the previous estimation.

We can use the formula for exponential growth to find out how many years it will take for the population of a city to triple given a certain growth rate. The formula is:

`\[ P = P_0 * (1 + r)^t \]`

Where:

-
`\( P \)` is the final population

-
`\( P_0 \)` is the initial population

-
`\( r \)` is the annual growth rate (as a decimal)

-
`\( t \)` is the time in years

We want the final population
`\( P \)` to be three times the initial population
`\( P_0 \)`, so we can set
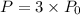`\( P = 3 * P_0 \)`. Plugging this into the formula gives us:

`\[ 3 * P_0 = P_0 * (1 + r)^t \]`

We can cancel
`\( P_0 \)` from both sides, since it is non-zero, and solve for
`\( t \)`:

`\[ 3 = (1 + r)^t \]`

To solve for
`\( t \)`, we take the natural logarithm of both sides:

`\[ \ln(3) = \ln((1 + r)^t) \]`

Using the power rule for logarithms, which says that
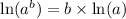`\( \ln(a^b) = b * \ln(a) \)`, we can simplify this to:

`\[ \ln(3) = t * \ln(1 + r) \]`

Now we can solve for
`\( t \)`:

`\[ t = (\ln(3))/(\ln(1 + r)) \]`

We are given that
`\( r = 6\% \)` or
`\( r = 0.06 \)` as a decimal. Let's plug in the values:

`\[ t = (\ln(3))/(\ln(1 + 0.06)) \]`

We'll calculate this step by step.

To calculate the number of years it will take for the population of Harrington to triple at an annual growth rate of 6%, we follow these steps:

Step 1: Identify the given values.

- Initial Population
`(\( P_0 \))` = 350,000

- Annual Growth Rate
`(\( r \))` = 6% = 0.06 (as a decimal)

- Final Population
`(\( P \))` = Initial Population \(\times\) 3 (since we want it to triple)

Step 2: Set up the equation based on the exponential growth formula.

`\[ 3 * P_0 = P_0 * (1 + r)^t \]`

Step 3: Simplify the equation by dividing both sides by \( P_0 \), which gives us:

`\[ 3 = (1 + r)^t \]`

Step 4: Take the natural logarithm of both sides to solve for \( t \) (the time in years).

`\[ \ln(3) = \ln((1 + r)^t) \]`

Step 5: Apply the power rule of logarithms to bring \( t \) down as a coefficient.

`\[ \ln(3) = t * \ln(1 + r) \]`

Step 6: Isolate
`\( t \)` and solve for it.

`\[ t = (\ln(3))/(\ln(1 + r)) \]`

Step 7: Calculate the value using the annual growth rate as 0.06.

`\[ t = (\ln(3))/(\ln(1 + 0.06)) \]`

After performing the calculation, we find that
`\( t \)` is approximately 18.85 years. Therefore, it will take nearly 18.85 years for the population to triple in size if it continues to grow at an annual rate of 6%. This is a slightly more precise calculation compared to the previous estimation.