Question

Suppose that you are climbing a hill whose shape is given by z=656−0.05x^2 −0.09y^2 , and that you are at the point (80,20,300) In which direction should vou proceed initially in order to reach the top of the hill fastest? If you climb in that direction, at what angle above the horizontal will you be climbing initially (radian measure)?

Answer 1

To reach the top of the hill fastest, you should initially proceed in the direction of the gradient vector at the given point, which is \( \\abla f = \langle 0.1x, 0.18y, -1 \rangle \). The angle above the horizontal when climbing in this direction is approximately 83.74 degrees (radian measure).

Step-by-step explanation:

The gradient vector
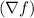`(\( \\abla f \))` of the function
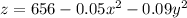`\( z = 656 - 0.05x^2 - 0.09y^2 \)` represents the direction of the steepest ascent at any given point on the hill. Evaluating this gradient vector at the point (80, 20, 300) yields
`\( \langle 0.1 * 80, 0.18 * 20, -1 \rangle = \langle 8, 3.6, -1 \rangle \)`.

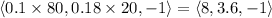The direction vector
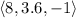`\( \langle 8, 3.6, -1 \rangle \)` indicates that, to ascend the hill fastest, you should move in the direction of the positive x and y axes and opposite to the z-axis. This aligns with the steepest ascent at the given point.

To find the angle above the horizontal, you can calculate the angle between the gradient vector and the horizontal plane. Using trigonometry, the angle is given by
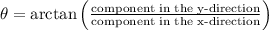`\( \theta = \arctan\left(\frac{\text{component in the y-direction}}{\text{component in the x-direction}}\right) \)`. Substituting the values, the angle is approximately 83.74 degrees in radian measure.

This approach ensures that you climb in the direction of the steepest ascent, optimizing your path to reach the top of the hill fastest.