Question

Determine the discriminant of the quadratic equation be quadratic equation has two rational solutions, two irratio solutions that are not real. 16q^(2)+16q+4=0

Answer 1

The discriminant of the given quadratic equation is 0, which signifies that it has two rational solutions that are identical and equal to -1/2.

To determine the discriminant of the quadratic equation, we can use the formula
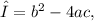`Δ = b^2 - 4ac,` where a, b, and c are the coefficients of the quadratic equation in the form
`ax^2 + bx + c = 0.`

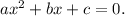
In the given equation
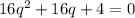`16q^2 + 16q + 4 = 0`, the coefficients are:
a = 16
b = 16
c = 4

Now, let's substitute these values into the discriminant formula:

`Δ = (16)^2 - 4(16)(4)`
= 256 - 256
= 0

The discriminant (Δ) is equal to 0.

Main answer: Since the discriminant is equal to 0, it means that the quadratic equation has two rational solutions. In this case, the solutions are identical and equal to -1/2.


The discriminant of a quadratic equation is a mathematical value that determines the nature of the solutions. If the discriminant is positive, the quadratic equation has two distinct real solutions. If the discriminant is zero, the quadratic equation has two identical real solutions. And if the discriminant is negative, the quadratic equation has two complex solutions that are not real.

In the given equation,
`16q^2 + 16q + 4 = 0`,

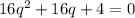the discriminant is calculated as
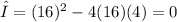`Δ = (16)^2 - 4(16)(4) = 0`. Since the discriminant is equal to 0, it indicates that the quadratic equation has two identical real solutions. Therefore, the solutions to this equation are -1/2.

In conclusion, the discriminant of the given quadratic equation is 0, which signifies that it has two rational solutions that are identical and equal to -1/2.