Question

Use the functions f(x)=x−3 and g(x)=x2−2x−3 to evaluate the expressions shown below, simplifying your answers completely: (a) Find f(x)−g(x) (b) Find (f∘g)(x)−(g∘f)(x)

Answer 1

Given two functions $f(x) = x-3$ and $g(x) = x^2 - 2x - 3$

There are two problems to solve :

a) Find $f(x) - g(x)$

b) Find $(f \cdot g)(x) - (g \cdot f)(x)$

A. Find $f(x) - g(x)$

`(x-3) - (x^2 - 2x - 3) = x - 3 - x^2 + 2x + 3 \\ = 3x - x^2`

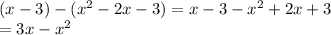
The answer for A is $3x - x^2$

B. Calculate $(f \cdot g)(x) - (g \cdot f)(x)$

First we calculate for $(f \cdot g)(x)$

`(f \cdot g)(x) &=& (x^2 - 2x - 3) - 3 \\ &=& x^2 - 2x - 6`

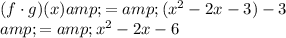
Then we calculate for $(g \cdot f)(x)$

`(g \cdot f)(x) &=& (x-3)^2 - 2(x-3) - 3 \\ &=& x^2 - 6x + 9 - 2x + 6 - 3 \\ &=& x^2 - 8x + 12`

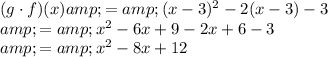
We can then calculate $(f \cdot g)(x) - (g \cdot f)(x)$

`&=& (x^2 - 2x - 6) - (x^2 - 8x + 12) \\ &=& x^2 - 2x - 6 - x^2 + 8x - 12 \\ &=& 6x - 18`

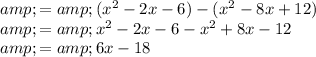
Therefore the answer for B is $6x-18$