Question

a force of 225 newtons stretches a spring 15 centimeters. how much work is done in stretching the spring from 22 centimeters to 39 centimeters? be sure to give your answer in joules. you may give your answer as a decimal.

Answer 1

`77.775\; {\rm J}`.

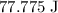Step-by-step explanation:

Note the unit conversion: standard unit of distance should be meters, not centimeters.

Divide the restoring force
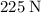`225\; {\rm N}` by the displacement
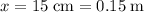`x = 15\; {\rm cm} = 0.15\; {\rm m}` of the spring to find the spring constant:

`\displaystyle k = \frac{225\; {\rm N}}{0.15\; {\rm m}} = 1500\; {\rm N\cdot m^(-1)}`.

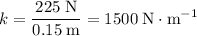When the displacement of the spring is
`x`, the elastic potential energy stored in this spring would be
`(1/2)\, k\, x^(2)`. Subtract the initial value of elastic potential energy from the new one to find the energy required:

`\begin{aligned} & (1)/(2)\, k\, {x_(1)}^(2) - (1)/(2)\, k\, {x_(0)}^(2) \\ =\; & (1)/(2)\, k\, ({x_(1)}^(2) - {x_(0)}^(2)) \\ =\; & (1)/(2)\, (1500)\, (0.39^(2) - 0.22^(2)) \; {\rm N\cdot m} \\ =\; & 77.775\; {\rm J}\end{aligned}`.

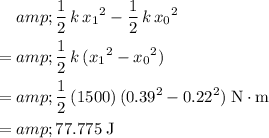In other words, the energy required to stretch the spring would be
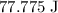`77.775\; {\rm J}`.