The two throws that cause the javelin to land the same distance away are:
1. The throws at 30° and 60°.
2. The throws at 40° and 50°.
To determine which two throws cause the javelin to land the same distance away, we need to consider the range of a projectile. The range
 of a projectile launched at an angle
of a projectile launched at an angle
 with an initial speed
with an initial speed
 can be calculated using the formula:
can be calculated using the formula:
![\[R = (v_0^2 \sin(2\theta))/(g),\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/2x0u19b8g69vp5b7u3f2jagg7lkx7r1n0f.png)
where
 is the acceleration due to gravity.
is the acceleration due to gravity.
In this case, the athlete throws the javelin at four different angles with the same speed. Let's denote the initial speed as
 (which is the same for all throws). We can compare the ranges for different angles.
(which is the same for all throws). We can compare the ranges for different angles.
1. For an angle of 30°
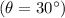 :
:
![\[R_(30) = (v_0^2 \sin(2 * 30^\circ))/(g).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ra34ukhh0q8jiou8dogqcv3lrayl0040rr.png)
2. For an angle of 40°
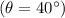 :
:
![\[R_(40) = (v_0^2 \sin(2 * 40^\circ))/(g).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/g34lalv1ibnn8gos1v31w8owa62jgjapvj.png)
3. For an angle of 60°
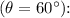
![\[R_(60) = (v_0^2 \sin(2 * 60^\circ))/(g).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/fa8ftkmnbafha0om0ctkpk9njnevus1btp.png)
4. For an angle of 80°
 :
:
![\[R_(80) = (v_0^2 \sin(2 * 80^\circ))/(g).\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/9k56ccu0d4f4eh5e3mf3hcm6u7w1ir1eoc.png)
Now, we can compare these ranges and identify pairs that are equal.
Without specific numerical values, we can make some observations:
- The ranges for angles
 are equal because
are equal because
 .
.
- The ranges for angles
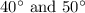 are also equal because
are also equal because
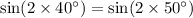 .
.