Answer:
Explanation:
We are given an equation:
And we are asked to find all real zeros and state the multiplicity of each.
- When f(x) = 0, the values of x are the zeros of a function.
To find the real zeros, you need set each variable equal to zero, the solve for the variable x.
The exponents value is the multiplicity of the zeros.
----
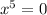
![\sqrt[5]{x^5} =\sqrt[5]{0} \\](https://img.qammunity.org/2024/formulas/mathematics/high-school/x35rbg4jc8y5z25ol8oo0xawydmcmy4ftu.png)
x = 0 multiplicity of 5
----
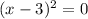
![\sqrt[2]{(x-3)^2} =\sqrt[2]{0} \\x-3 = 0\\](https://img.qammunity.org/2024/formulas/mathematics/high-school/q2f84wbdcw62yynagu58xslxia5qr36zya.png)
x = 3 multiplicity of 2
----

x = -8 multiplicity of 1
----