Question

Consider the following measurement problem. The measurement equation is y = 2x1 + 4x2^2;

x1 = 25cm +- 3%
x2 = 50cm +-5%
Calculate the following and enter your answers into the quiz questions. Use the SRSS method.
The nominal measureand
The fractional error for x1
The fractional error for x2
The fractional error in y

Answer 1

Nominal measure for y: 10,050 cm, Fractional error for x₁: 3%, Fractional error for x₂: 0.2, and Fractional error in y: 20.23%

To calculate the nominal measure and fractional errors for the given measurement problem, we will use the SRSS (Square Root of the Sum of Squares) method. The fractional error is expressed as a percentage.

Nominal measure for y:

The nominal measure for y can be calculated by substituting the given values of x₁ and x₂ into the measurement equation.

`y = 2x_1 + 4x_2^2`

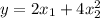
Substituting x₁ = 25 cm and x₂ = 50 cm into the equation:

`y = 10050 \:\:cm`

Therefore, the nominal measure for y is 10,050 cm.

Fractional error for x₁:

The fractional error for x₁ is given as 3% (0.03). Since the measurement equation for y only includes x₁ in a linear form, the fractional error for x₁ is directly carried over to y.

Therefore, the fractional error for x₁ is 3%.

Fractional error for x₂:

The fractional error for x₂ is given as 5% (0.05). However, in the measurement equation for y, x₂ is squared. To propagate the fractional error, we multiply the fractional error by the power of 2:

Fractional error for x₂ in
`y = 2 * (2) * 0.05 = 0.2`

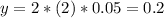
Therefore, the fractional error for x₂ in y is 0.2.

Fractional error in y:

To calculate the fractional error in y, we use the SRSS method (Square Root of the Sum of Squares) to combine the fractional errors of x₁ and x₂ in y.

Fractional error in

`y = √(0.03^2 + 0.2^2)=0.2023`

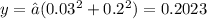
Therefore, the fractional error in y is approximately 20.23%.