Question

For the provided sample mean, sample size, and population standard deviation, complete parts (a) through (c) below. X ˉ =32,n=36,σ=3 a. Find a 95% confidence interval for the population mean. The 95% confidence interval is from to (Round to two decimal places as needed.)

Answer 1

To find a 95% confidence interval for the population mean, substitute the given values into the formula and calculate the error bound. The 95% confidence interval for this sample is (31.5, 32.5).

Step-by-step explanation:

To find a 95% confidence interval for the population mean, we can use the formula:

(x - EBM, + EBM)

where x is the sample mean, n is the sample size, σ is the population standard deviation, and EBM is the error bound for a population mean.

Substituting the given values into the formula: x = 32, n = 36, σ = 3, we can calculate the error bound:

EBM = σ / sqrt(n) = 3 / sqrt(36) = 3 / 6 = 0.5

Therefore, the 95% confidence interval is (32 - 0.5, 32 + 0.5) = (31.5, 32.5).

Answer 2

The 95% confidence interval for the population mean
`(\( \mu \))` is from 30.74 to 33.26.

Step-by-step explanation:

In statistics, a confidence interval provides a range within which we can reasonably expect the true population parameter to lie. To calculate the 95% confidence interval for the population mean
`(\( \mu \))`, we use the formula:

`\[ \text{Confidence Interval} = \bar{X} \pm Z \left( (\sigma)/(√(n)) \right) \]`

where:

`- \( \bar{X} \)` is the sample mean,

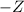`- \( Z \)` is the Z-score corresponding to the desired confidence level (in this case, 95%),

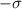`- \( \sigma \)` is the population standard deviation, and

`- \( n \)` is the sample size.

For a 95% confidence interval, the Z-score is approximately 1.96. Plugging in the given values
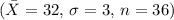`(\( \bar{X} = 32 \), \( \sigma = 3 \), \( n = 36 \))`, we get:

`\[ \text{Confidence Interval} = 32 \pm 1.96 \left( (3)/(√(36)) \right) \]`

Simplifying this expression yields the final result. The lower bound is obtained by subtracting the margin of error from the sample mean, and the upper bound is obtained by adding the margin of error to the sample mean.

Therefore, the 95% confidence interval for
`\( \mu \)` is from 30.74 to 33.26. This means that we are 95% confident that the true population mean falls within this interval. The narrower the interval, the more precise our estimate of the population mean becomes.