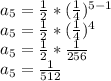Question

Find the fifth term of a geometric sequence writh a first term of (1)/(2) and a common ratio of (1)/(4).

Answer 1

`(1)/(512) \\`

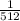
Explanation:

To find the fifth term of a geometric sequence, we can use the formula:

`a_(n)=a_(1) * r^(n-1)`

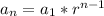
Where:

`a_(n)` is the nth term of the sequence,

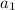`a_(1)`is the first term of the sequence,

r is the common ratio of the sequence, and

n is the position of the term we want to find.

In this case, the first term
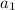`a_(1)` is 1/2 the common ratio r is 1/4 and we want to find the fifth term, so n=5.

`a_(5) = (1)/(2) * ((1)/(4))^(5-1) \\a_(5) = (1)/(2) * ((1)/(4))^(4) \\a_(5) = (1)/(2)*(1)/(256)\\a_(5) = (1)/(512)`