Question

I NEED HELP FAST

A bicycle chain is pulled tightly so that MN is a common tangent of the gears. Find the distance between the centres of the gears

Answer 1

17.8 in

Explanation:

The tangent of a circle is always perpendicular to the radius.

Therefore, if MN is a common tangent of circle L and circle P, and LM and PN are the radii of the circles, then ∠LMN is 90° and ∠PNM is 90°.

To find the distance between the center of the gears, we need to find the length of line segment LP.

LP is the hypotenuse of a right triangle with the measure of one leg equal to MN (17.6 in), and the measure of the other leg equal to the difference between the radii of the two circles. (See the attached diagram).

The difference between the radii of the two circle is:

4.3 - 1.8 = 2.5

To find LP, use Pythagoras Theorem.

`17.6^2+2.5^2=LP^2`

`309.76+6.25=LP^2`

`316.01=LP^2`

`LP^2=316.01`

`LP=17.7766701...`

`LP=17.8\;\sf in\;(nearest\;tenth)`

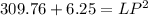
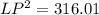
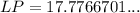
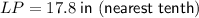
Therefore, the distance between the center of the gears is 17.8 in (rounded to the nearest tenth).