Question

Einstein's famous equation relating mass and energy is E=mc ^2 where c is the velocity of light (c=2.998×10 ^8 m/sec). Use this equation to calculate the energy equivalent of 1 amu.

Answer 1

Approximately
`1.495 * 10^(-10)\; {\rm J}`.

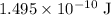Step-by-step explanation:

Atomic mass unit (
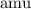`{\rm amu}`) is a unit for mass. In standard unit, one atomic mass unit is equivalent to approximately
`1.661 * 10^(-27)\; {\rm kg}`.

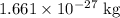Substitute
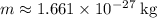`m \approx 1.661 * 10^(-27)\; {\rm kg}` and
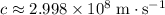`c \approx 2.998 * 10^(8)\; {\rm m\cdot s^(-1)}` into the equation:

`\begin{aligned}E &= m\, c^(2) \\ &\approx (1.661 * 10^(-27)\; {\rm kg})\, (3.00 * 10^(8)\; {\rm m\cdot s^(-1)})^(2) \\ &\approx 1.495 * 10^(-10)\; {\rm kg \cdot m^(2)\cdot s^(-2)}\end{aligned}`.

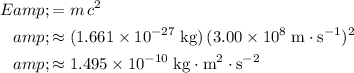Note that
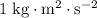`1\; {\rm kg\cdot m^(2)\cdot s^(-2)}` is equivalent to
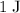`1\; {\rm J}` (one Joule.) Therefore, the energy equivalent to
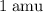`1\; {\rm amu}` would be approximately
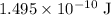`1.495 * 10^(-10)\; {\rm J}`.