Question

Who can solve this ? Pls help

Answer 1

Given:

• side of a regular octagon = 8cm

To find

• It's area

we know that,

• The area of a octagon = 2(1+√2) x side ²

Inserting the given value in the formula

• Area = 2(1+√2) x (8cm)²
• Area = 2+2√2 x 64 cm²
• Area = 4√2 x 64 cm²
• Area = 309.02 cm²

Answer 2

309.0 cm²

Explanation:

The formula for the area of a regular polygon, given its side length, is:

`\boxed{\begin{minipage}{5.5cm}\underline{Area of a regular polygon}\\\\$A=(s^2n)/(4 \tan\left((180^(\circ))/(n)\right))$\\\\\\where:\\\phantom{ww}$\bullet$ $n$ is the number of sides.\\ \phantom{ww}$\bullet$ $s$ is the side length.\\\end{minipage}}`

A regular octagon has 8 sides, so n = 8.

We are told that the side length is 8 cm, so s = 8.

Substitute the values of n and s into the formula and solve for area:

`\textsf{Area}=(8^2 \cdot 8)/(4 \tan\left((180^(\circ))/(8)\right))`

`\textsf{Area}=(64 \cdot 8)/(4 \tan\left((180^(\circ))/(8)\right))`

`\textsf{Area}=(512)/(4 \tan\left(22.5^(\circ)\right))`

`\textsf{Area}=(128)/(\tan\left(22.5^(\circ)\right))`

`\textsf{Area}=309.01933598...`

`\textsf{Area}=309.0\; \sf cm^2\;(nearest\;tenth)`

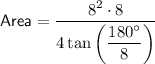
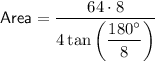
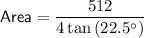
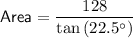
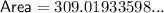
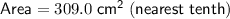
Therefore, the area of a regular octagon with a side length of 8 cm is 309.0 cm², rounded to the nearest tenth.