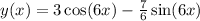Question

Solve the given initial value problem. y ′′
+36y=0,y(0)=3,y ′
(0)=−7 y(x)=

Answer 1

`y(x)=3\cos(6x)-(7)/(6)\sin(6x)`

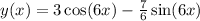
Explanation:

Solve the roots

`y''+36y=0\\r^2+36=0\\(r+6i)(r-6i)=0\\r=\pm6i`

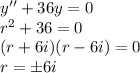
Because the roots are complex conjugates, then the general solution we'll need to use is
`y(x)=e^(\alpha x)[c_1\cos(\beta x)+c_2\sin(\beta x)]` where
`r=\alpha\pm\beta i`.

This makes the general solution
`y(x)=e^(0x)[c_1\cos(6x)+c_2\sin(6x)]=c_1\cos(6x)+c_2\sin(6x)`

Since
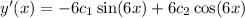`y'(x)=-6c_1\sin(6x)+6c_2\cos(6x)`, we can plug in our initial conditions into
`y(x)` and
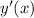`y'(x)` to solve for each constant:

`y(x)=c_1\cos(6x)+c_2\sin(6x)\\y(0)=c_1\cos(6\cdot0)+c_2\sin(6\cdot 0)\\3=c_1\cos(0)+c_2\sin(0)\\3=c_1`

`y'(x)=-6c_1\sin(6x)+6c_2\cos(6x)\\y'(0)=-6c_1\sin(6\cdot0)+6c_2\cos(6\cdot0)\\-7=-6(3)\sin(0)+6c_2\cos(0)\\-7=6c_2\\c_2=-(7)/(6)`

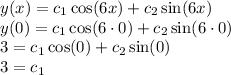
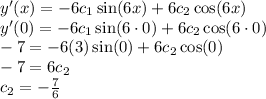
Therefore, the solution to the given IVP is
`y(x)=3\cos(6x)-(7)/(6)\sin(6x)`