To calculate confidence intervals for the variance
 and the standard deviation
and the standard deviation
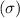 of the Lysine composition levels in soybean meals, we'll use the Chi-Square distribution.
of the Lysine composition levels in soybean meals, we'll use the Chi-Square distribution.
Given data:
Column A: 22.2, 24.7, 20.9, 26.0, 27.0
Column B: 24.8, 26.5, 23.8, 25.6, 23.9
Let's first calculate the sample variance
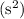 of the Lysine composition levels.
of the Lysine composition levels.
Step 1: Calculate the sample variance.
Sample variance formula:
![\[ s^2 = \frac{\sum (x_i - \bar{x})^2}{n - 1} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/nolvxmq73rh8hwnsb5v37nea91lramchbj.png)
Where:
 each value in the sample
each value in the sample
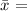 sample mean
sample mean
 number of observations
number of observations
For Column A:
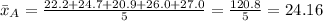
![\[ s_A^2 = ((22.2 - 24.16)^2 + (24.7 - 24.16)^2 + (20.9 - 24.16)^2 + (26.0 - 24.16)^2 + (27.0 - 24.16)^2)/(5 - 1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/4er0jgada9mtileqzma2q05jk8bbsen5ew.png)
![\[ s_A^2 = (4.0256 + 0.0289 + 12.0964 + 3.3664 + 8.6436)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/tb6myhbkjrz9wwpmwr1x6igoso31y7ngfr.png)
![\[ s_A^2 = (28.16)/(4) = 7.04 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/kcm18li3rj3gbfq3l2nwf5oxsgmwhmy5cv.png)
For Column B:
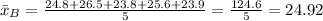
![\[ s_B^2 = ((24.8 - 24.92)^2 + (26.5 - 24.92)^2 + (23.8 - 24.92)^2 + (25.6 - 24.92)^2 + (23.9 - 24.92)^2)/(5 - 1) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/szosl1n40m1txx239az2381vhs1n163htu.png)
![\[ s_B^2 = (0.0144 + 2.4784 + 1.3664 + 2.0736 + 1.0564)/(4) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/w3j74y7k7d5rytlgi4fal3wxsvt80pe08b.png)
![\[ s_B^2 = (7.9892)/(4) = 1.9973 \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/h67q5jwtj7fv6jmhvu7phu13spchys27hl.png)
Step 2: Calculate the degrees of freedom.
Degrees of freedom
 for sample variances is
for sample variances is
 .
.
For both Column A and Column B,
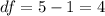 .
.
(a) Construct a 99% two-sided confidence interval for
 .
.
The formula for the confidence interval for variance using Chi-Square distribution is:
![\[ \left( ((n-1)s^2)/(\chi^2_(\alpha/2)), ((n-1)s^2)/(\chi^2_(1-\alpha/2)) \right) \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ufpg3qji8oxdnmsfqyn60ajmeqnxuuez49.png)
Where
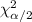 and
and
 are the Chi-Square critical values at
are the Chi-Square critical values at
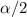 and
and
 percentiles respectively with
percentiles respectively with
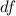 degrees of freedom.
degrees of freedom.
For a 99% confidence interval with
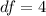 , the critical values are
, the critical values are
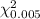 and
and
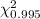 .
.
We need to find these critical values using a Chi-Square distribution table or statistical software.
For
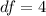 :
:
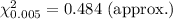
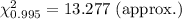
Now plug these values into the formula for both Column A and Column B:
For Column A:
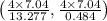
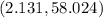
For Column B:

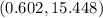
(b) Calculate a 99% lower confidence bound for
 .
.
The lower confidence bound for variance is simply the lower limit of the confidence interval, which is the first value in the interval.
For Column A: Lower bound
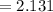
For Column B: Lower bound
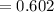
(c) Calculate a 95% lower confidence bound for
 .
.
The formula for the lower confidence bound for standard deviation
 from the variance
from the variance
 is:
is:
![\[ \sqrt{\text{Lower bound of } \sigma^2} \]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yqf2y3xq3bxwohb7he2sz0yaq5y9q499z7.png)
For Column A:

For Column B:
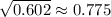
These values represent the lower bounds for the standard deviation
 at 95% confidence level.
at 95% confidence level.
An article in the Australion Journal of Agricultural Research, "Non-Starch Polysaccharides and Broiler Performance on Diets Containing Soyabean Meal as the Sole Protein Concentrate
 determined the essential amino acid (Lysine) composition level of soybean meals are as shown below (g/kg):
determined the essential amino acid (Lysine) composition level of soybean meals are as shown below (g/kg):
Round your answers to 2 decimal places.
(a) Construct a
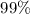 two-sided confidence interval for
two-sided confidence interval for
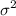 .
.
(b) Calculate a
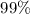 lower confidence bound for
lower confidence bound for
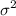
(c) Calculate a
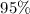 lower confidence bound for
lower confidence bound for
 .
.
The table is given below: