Question

In 2020, of 60 randomly selected Fortune 500 companies in the United States, 2 had a CEO who was Black. Determine a 95% confidence interval for the true proportion of all Fortune 500 companies in the United States that have a Black CEO.

Answer 1

The 95% confidence interval for the true proportion of all Fortune 500 companies in the United States that have a Black CEO is approximately (-0.0536, 0.1202).

To determine a confidence interval for the true proportion of all Fortune 500 companies in the United States that have a Black CEO, we can use the formula for a confidence interval for a proportion.

Given that out of the 60 randomly selected companies, 2 had a Black CEO, the sample proportion is 2/60 = 0.0333.

To calculate the confidence interval, we need to determine the standard error of the proportion. The formula for the standard error of a proportion is:

`\rm SE = \sqrt{(\hat p * (1 - \hat p) / n)`

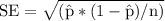
Where:

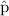`\rm \hat p` is the sample proportion

n is the sample size

In this case,
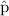`\rm \hat p` = 0.0333 and n = 60.

`SE = √((0.0333 * (1 - 0.0333)) / 60 \approx 0.0443)`

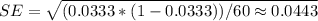
Next, we can calculate the margin of error by multiplying the standard error by the critical value corresponding to the desired confidence level. For a 95% confidence level, the critical value is approximately 1.96.

Margin of Error = 1.96 * SE ≈ 1.96 * 0.0443 ≈ 0.0869

Finally, we can construct the confidence interval by subtracting and adding the margin of error to the sample proportion:

Confidence Interval =
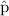`\rm \hat p` ± Margin of Error

Confidence Interval = 0.0333 ± 0.0869

Therefore, the 95% confidence interval for the true proportion of all Fortune 500 companies in the United States that have a Black CEO is approximately (-0.0536, 0.1202).

Know more about