The expected heart rate of the Eastern Bearded Dragon Lizard at a body temperature of 39 degrees Celsius is approximately 67.58 beats per minute.
To estimate the heart rate at a different temperature using the Arrhenius equation, we need to understand the equation itself:
![\[ k = A \exp\left(-(E_a)/(RT)\right) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/2tcyem5uthl82amxpbnl53530pla6qj1ac.png)
where:
-
 is the rate constant (which in this context we can relate to the heart rate),
is the rate constant (which in this context we can relate to the heart rate),
-
 is the pre-exponential factor (a constant),
is the pre-exponential factor (a constant),
-
 is the activation energy,
is the activation energy,
-
 is the gas constant (8.314 J/(mol·K)),
is the gas constant (8.314 J/(mol·K)),
-
 is the temperature in Kelvin.
is the temperature in Kelvin.
We can rearrange the Arrhenius equation to compare the rate constants (heart rates) at two different temperatures:
![\[ \ln\left((k_2)/(k_1)\right) = (-E_a)/(R)\left((1)/(T_2) - (1)/(T_1)\right) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/4bsq1mls1nuk9u29jva3xm8p6m202r7evk.png)
However, we do not know the activation energy
 for the heart rate temperature dependence. But we can solve for
for the heart rate temperature dependence. But we can solve for
 using the heart rates and temperatures provided, and then use that to find the heart rate at the new temperature.
using the heart rates and temperatures provided, and then use that to find the heart rate at the new temperature.
First, convert all temperatures to Kelvin by adding 273.15 to the Celsius temperatures:
-
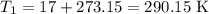
-
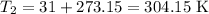
-
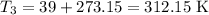
Then, using the given heart rates
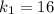 beats/min and
beats/min and
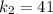 beats/min, we can solve for
beats/min, we can solve for
 . Let's start by solving for
. Let's start by solving for
 using the first two temperatures and heart rates.
using the first two temperatures and heart rates.
The calculated activation energy
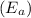 for the heart rate temperature dependence is approximately
for the heart rate temperature dependence is approximately
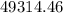 J/mol.
J/mol.
Now, we can use this activation energy to estimate the heart rate at 39 degrees Celsius (or 312.15 K). We'll use the following rearranged Arrhenius equation to solve for the new heart rate
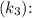
![\[ \ln\left((k_3)/(k_1)\right) = (-E_a)/(R)\left((1)/(T_3) - (1)/(T_1)\right) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/rod04vw6sodo0o65pbxk8an7lv4gtxgk2i.png)
First, we solve for
 and then calculate
and then calculate
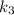 :
:
![\[ k_3 = k_1 * \exp\left((-E_a)/(R)\left((1)/(T_3) - (1)/(T_1)\right)\right) \]](https://img.qammunity.org/2024/formulas/chemistry/high-school/j49r03ba77ij027jw87h5eccj2irjwoeba.png)
By performing this calculation using the activation energy we found and the temperature corresponding to 39 degrees Celsius.
Hence, the expected heart rate of the Eastern Bearded Dragon Lizard at a body temperature of 39 degrees Celsius is approximately 67.58 beats per minute.