Question

Acid precipitation dripping on limestone produces carbon dioxide by the following reaction: CaCO3(s)+2H+(aq)⟶Ca2+(aq)+CO2(g)+H2O(l) 15.0 mL of CO2 was produced at 25.0∘C and 730.0 mmHg. How many moles of CO2 were produced? mol Part 2 How many milligrams of CaCO3 were consumed?

Answer 1

The mass of CaCO3 consumed to produce the CO2 was approximately 58.91 milligrams.

To solve this two-part problem, we'll perform calculations based on the chemical reaction provided and the Ideal Gas Law for the conditions given. Here are the steps:

Part 1: Calculate the Moles of CO2 Produced

Step 1: Convert the Given Volume to Liters

- Since volume is given in milliliters, we need to convert it to liters because the Ideal Gas Law uses volume in liters.

`\[ 15.0 \text{ mL} = 15.0 * 10^(-3) \text{ L} \]`

Step 2: Convert Pressure to Atmospheres

- The Ideal Gas Law requires pressure in atmospheres. Convert the given pressure from mmHg to atmospheres.

`\[ 730.0 \text{ mmHg} * \frac{1 \text{ atm}}{760 \text{ mmHg}} \]`

Step 3: Convert Temperature to Kelvin

- The Ideal Gas Law requires temperature in Kelvin.

`\[ 25.0°C = 25.0 + 273.15 \text{ K} \]`

Step 4: Use the Ideal Gas Law to Find Moles of CO2

- The Ideal Gas Law is
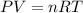`\( PV = nRT \)`, where
`\( P \)` is pressure,
`\( V \)` is volume,
`\( n \)` is number of moles,
`\( R \)` is the gas constant, and
`\( T \)` is temperature.

- Solve for
`\( n \)` (number of moles of CO2).

`\[ n = (PV)/(RT) \]`

Let's perform these calculations.

The number of moles of CO2 produced was approximately
`\( 5.89 * 10^(-4) \) moles.`

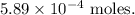
Part 2: Calculate the Milligrams of CaCO3 Consumed

Step 5: Determine the Molar Mass of CaCO3

- The molar mass of CaCO3 (calcium carbonate) is the sum of the atomic masses of its constituent atoms (Ca, C, and 3 O atoms).

Step 6: Calculate the Mass of CaCO3 Consumed

- Since the reaction between CaCO3 and H+ is a 1:1 molar ratio, the moles of CO2 produced will be the same as the moles of CaCO3 consumed.

- Convert the moles of CaCO3 to milligrams by multiplying with the molar mass of CaCO3 and then converting grams to milligrams by multiplying by 1000.

The mass of CaCO3 consumed to produce the CO2 was approximately 58.91 milligrams.

Answer 2

1. The number of mole of
`CO_2` produced is 0.0006 mole

2. The mass (in milligrams) of
`CaCO_3` consumed is 60 milligrams

How to calculate the mole and mass?

1. The number of mole of
`CO_2` produced can be calculated as follow:

• Volume of of
  `CO_2` (V) = 15 mL = 15 / 1000 = 0.015 L
• Temperature (T) = 25 °C = 25 + 273 = 273 K
• Pressure (P) = 730 mmHg = 730 / 760 = 0.961 atm
• Gas constant (R) = 0.0821 atm.L/mol K
• Number of mole of
  `CO_2` (n) =?

PV = nRT

0.961 × 0.015 = n × 0.0821 × 298

0.014415 = n × 24.4658

Divide both sides by 24.4658

n = 0.014415 / 24.4658

= 0.0006 mole

2. The mass (in milligrams) of
`CaCO_3` consumed can be calculated as follow:

First, we shall obtain the mole of
`CaCO_3` from the reaction. Details below:

`CaCO_3(s)\ +\ 2H^+(aq)\ \rightarrow\ Ca^(2+)(aq)\ +\ CO_2(g)\ +\ H_2O(l)`

From the balanced equation above,

1 mole of
`CO_2` , were produced from 1 mole of
`CaCO_3`

Therefore,

0.0006 mole of
`CO_2` will also be produce from 0.0006 mole of
`CaCO_3`

Now, we shall calculate the mass of
`CaCO_3`. Details below:

• Mole of
  `CaCO_3` = 0.0006 mole
• Molar mass of
  `CaCO_3` = 100 g
• Mass of
  `CaCO_3` =?

Mass of
`CaCO_3` = Mole × molar mass

= 0.0006 × 100

= 0.06 g

Multiply by 1000 to express in milligrams

= 0.06 × 1000

= 60 milligrams