The linear approximation is

The value of
![\sqrt[3]{28.45}](https://img.qammunity.org/2024/formulas/mathematics/high-school/ozl7ecoto53v1cvjycadcrvtgh4iqiv3mv.png)
is 3.054.
How to determine approximated value of a function
Given
![f(x) = \sqrt[3]{x}](https://img.qammunity.org/2024/formulas/mathematics/college/k2d2fdmfbtli7tgibzr9qtlen1nhhvypye.png)
To linearize the function at x = 27
L(x) = f(a) + f'(a) * (x - a)
L(x) is the linear approximation function.
f(x) is the original function.
a is the point around which we are linearizing.
f'(a) is the derivative of f(x) evaluated at a.
x is the variable.
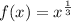
![= \sqrt[3]{27 } = 3](https://img.qammunity.org/2024/formulas/mathematics/high-school/bz8jtpr095sggsl6gmyjkvd9n9xogwqluu.png)
Find f'(x)
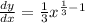
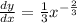
![= (1)/(3) {27}^{ - (2)/(3) } = (1)/(3) { (\sqrt[3]{27} }^( ) - 2)](https://img.qammunity.org/2024/formulas/mathematics/high-school/j0bqgkrsgkm7zqrmd3k8pxl0z1jet4285q.png)
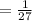
L(x) = f(a) + f'(a) * (x - a)
Substitute
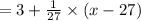

To approximate
![\sqrt[3]{28.45}](https://img.qammunity.org/2024/formulas/mathematics/high-school/ozl7ecoto53v1cvjycadcrvtgh4iqiv3mv.png)
x = 28.45
Therefore
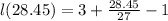
= 3 + 1.0536 -1
= 3.054
Therefore, approximated value is 3.054