Question

Find the linear approximation for f(x)=cos (2 x) at x=\frac{\pi}{6} . Use the linear approximation to approximate the value of cos (\frac{1}{2}) . Please enter your answer

Answer 1

The linear approximation to estimate the value of
`\( \cos\left((1)/(2)\right) \)` is approximately
`\( 0.541 \)` with three significant digits after the decimal point.

To find the linear approximation of
`\( f(x) = \cos(2x) \)` at
`\( x = (\pi)/(6) \)`, we first compute the derivative
`\( f'(x) \)`, and then use the point-slope form of the linear approximation:

1. Compute the derivative of
`\( f(x) \)`:

`\[ f'(x) = (d)/(dx)(\cos(2x)) = -2\sin(2x) \]`

2. Evaluate
`\( f(x) \)` and
`\( f'(x) \)` at
`\( x = (\pi)/(6) \)`:

`\[ f\left((\pi)/(6)\right) = \cos\left(2 \cdot (\pi)/(6)\right) = \cos\left((\pi)/(3)\right) = (1)/(2) \]`

`\[ f'\left((\pi)/(6)\right) = -2\sin\left(2 \cdot (\pi)/(6)\right) = -2\sin\left((\pi)/(3)\right) = -√(3) \]`

3. The linear approximation
`\( L(x) \)` near
`\( x = (\pi)/(6) \)` is:

`\[ L(x) = f\left((\pi)/(6)\right) + f'\left((\pi)/(6)\right)(x - (\pi)/(6)) \]`

`\[ L(x) = (1)/(2) - √(3)\left(x - (\pi)/(6)\right) \]`

4. Use the linear approximation to estimate
`\( f\left((1)/(2)\right) \)`:

`\[ L\left((1)/(2)\right) = (1)/(2) - √(3)\left((1)/(2) - (\pi)/(6)\right) \]`

The approximation yields
`\( L\left((1)/(2)\right) \approx 0.541 \)`.

Therefore, The answer is 0.541.

The complete question is here:

Find the linear approximation for
`f(x)=cos (2 x)` at
`x=(\pi)/(6)` . Use the linear approximation to approximate the value of cos
`((1)/(2))` . Please enter your answer

Answer 2

The linear approximation is

`- √(3)x + ( √(3)\pi )/(6) + (1)/(2)`

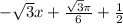
The appropriated value of

`\cos( (1)/(2) )`

is 0.974.

How to linearize a function.

The formula for linear approximation, also known as linearization, is given by:

L(x) = f(a) + f'(a) * (x - a)

L(x) is the linear approximation function.

f(x) is the original function.

a is the point around which you are linearizing.

f'(a) is the derivative of f(x) evaluated at a.

x is the variable.

Given f(x) = cos2x at π/6

when x = π/6

f(π/6) = cos(2*π/6)

= cos(π/3) or cos60⁰

= 1/2

f'(x) = derivative of f(x)

f'(x) = -2sin2x

When x = π/6

f'(π/6) = -2sin(2*π/6)

= -2sin(π/3) or sin60⁰

= -2*√3/2

= -√3

L(x) = f(a) + f'(a) * (x - a)

= 1/2 + (-√3)(x - π/6)

= 1/2 - √3x + (√3 π)/6

= -√3x + √3π/6 + 1/2

To approximate cos(1/2).

compare the functions

cos(2x) and cos(1/2)

2x = 1/2

4x = 1

x = 1/4

Substitute x = 1/4 into L(x) to find cos

`(1)/(2)`

`cos( (1)/(2)) = - √(3)( (1)/(4)) + ( √(3)\pi )/(6) + (1)/(2)`

= 0.974

The approximated value of

`\cos( (1)/(2) )`

is 0.974