The value of
 that satisfies the given implication for all
that satisfies the given implication for all
 is
is
 .
.
To find a value of
 such that the implication
such that the implication
![\[|x+4| \leq 2 \Rightarrow \left|((x+1)^2)/(x+7)-3\right| > K|x+4|\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/92qh9ft47s1o0k5zsjashb4xtsect3522o.png)
is true, we need to analyze the given inequality for different cases of
 .
.
Step 1: Analyzing
 :
:
Case 1:
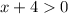
In this case,
 .
.
Case 2:
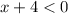
In this case,
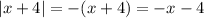 .
.
Step 2: Analyzing
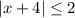 :
:
For Case 1:
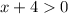
We have
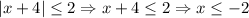 .
.
For Case 2:
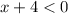
We have
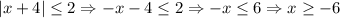 .
.
So, the condition
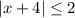 is satisfied when
is satisfied when
 or
or
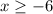 .
.
Step 3: Analyzing the inequality for each case:
Case 1:

In this case,
 and the given inequality becomes:
and the given inequality becomes:
![\[x+4 \leq 2 \Rightarrow x \leq -2\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ede0efph5p9hew0v328wmcuo4z4mjzsqcr.png)
Now, let's analyze the right side of the inequality:
![\[\left|((x+1)^2)/(x+7)-3\right| > K|x+4|\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/5pcho248ogvz9k0xdao69smw1m5lte7apj.png)
For
 , we know that
, we know that
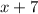 is also negative. So, let's consider two subcases:
is also negative. So, let's consider two subcases:
Subcase 1:
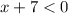
In this subcase,
 is negative, and the inequality becomes:
is negative, and the inequality becomes:
![\[-\left(((x+1)^2)/(x+7)-3\right) > K(x+4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/z9r08dm4rtz2eduwyelx3dhze4fvxiw9g4.png)
Now, simplify the left side:
![\[3 - ((x+1)^2)/(x+7) > K(x+4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cxx7cjnhld37a902krc457xm4lkuolfog2.png)
Subcase 2:

In this subcase,
 is positive, and the inequality becomes:
is positive, and the inequality becomes:
![\[((x+1)^2)/(x+7)-3 > K(x+4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yxy64wewmokcfnqwkq7ve7c8j0hqom0mf5.png)
Now, let's analyze each subcase separately.
Subcase 1:
![\[3 - ((x+1)^2)/(x+7) > K(x+4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/cxx7cjnhld37a902krc457xm4lkuolfog2.png)
To find the maximum value of
 for
for
 , we need to maximize
, we need to maximize
 by setting
by setting
 . Thus, the maximum value of
. Thus, the maximum value of
 is
is
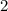 .
.
So, the inequality becomes:
![\[3 - ((x+1)^2)/(x+7) > 2K\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lbqta2tuvrp7491z97i337xmetoyqa2agg.png)
Subcase 2:
![\[((x+1)^2)/(x+7)-3 > K(x+4)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/yxy64wewmokcfnqwkq7ve7c8j0hqom0mf5.png)
To find the minimum value of
 for
for
 , we need to minimize
, we need to minimize
 by setting
by setting
 . Thus, the minimum value of
. Thus, the minimum value of
 is
is
 .
.
So, the inequality becomes:
![\[((x+1)^2)/(x+7)-3 > 0\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/lbxruvo4mes7hu9zzqkqzifisft76vlewc.png)
Now, we have analyzed the inequality for both subcases:
Subcase 1:
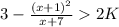
Subcase 2:
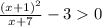
Step 4: Choosing the value of
 :
:
To ensure that the given implication is true for all
 , we need to choose a value of
, we need to choose a value of
 such that both subcases hold true.
such that both subcases hold true.
Subcase 1:
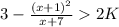
We want this inequality to hold true for all
 . To make it true for the entire range, we should choose the largest possible value for
. To make it true for the entire range, we should choose the largest possible value for
 .
.
To do that, we need to find the minimum value of the left side of the inequality, which occurs when
 :
:
![\[3 - ((-2+1)^2)/(-2+7) = 3 - (1)/(5) = (14)/(5)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/crc71h3otecpo6lmnvak0ndnma2huyskn3.png)
So, for this subcase to be true for all
 , we should choose
, we should choose
 such that:
such that:
![\[(14)/(5) > 2K\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/ge5kqp7uru4bicz3q94mabd93wewu0iy8k.png)
Solve for
 :
:
![\[K < (7)/(10)\]](https://img.qammunity.org/2024/formulas/mathematics/high-school/xkyjilz5o5wwngph3bbwyr6vcbbzplpvhu.png)
Subcase 2:
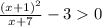
This inequality is already true for all
 , regardless of the value of
, regardless of the value of
 , because the left side is always positive.
, because the left side is always positive.
Now, we need to ensure that both subcases are satisfied. The maximum value of
 for Subcase 1 is
for Subcase 1 is
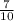 , and it does not affect Subcase 2.
, and it does not affect Subcase 2.
So, we can choose
 to be any value less than
to be any value less than
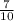 .
.
Therefore, one possible choice for
 is
is
 , which is less than
, which is less than
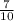 .
.
The complete question is here: