Question

What is the correct standard form of the equation of the parabola?

Enter your answer below. Be sure to show each step of your work for full credit?

Answer 1

`(x+3)^2=-4(y-3)`

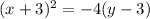
Explanation:

The given graph shows a parabola that opens downwards.

The directrix of a parabola is a fixed line outside of the parabola that is perpendicular to the axis of symmetry. Therefore, the directrix of the given parabola is y = 4.

The focus of a parabola is a fixed point located on the axis of symmetry, such that all points on the parabola are equidistant to both the focus and the directrix. It is located inside the parabola. Therefore, the focus of the given parabola is (-3, 2).

The vertex of a parabola is the maximum or minimum point of the curve (turning point). Therefore, the vertex of the given parabola is (-3, 3).

The standard form of a parabola with a vertical axis of symmetry is:

`\boxed{(x-h)^2=4p(y-k)}`

where:

• p ≠ 0
• Vertex = (h, k)
• Focus = (h, k+p)
• Directrix: y = (k - p)

Since the vertex of the graphed parabola is (-3, 3), then h = -3 and k = 3.

To find the value of p, substitute the found value of k into the formula for the directrix:

`\begin{aligned}\textsf{Directrix:} \quad y&=k-p\\4&=3-p\\p&=-1\end{aligned}`

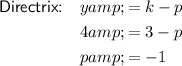
Finally, substitute the values of h, k and p into the standard formula:

`(x-(-3))^2=4(-1)(y-3)`

`(x+3)^2=-4(y-3)`

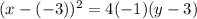
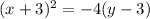
Therefore, the equation of the parabola in standard form is:

`\large\boxed{(x+3)^2=-4(y-3)}`

Answer 2

`\bold{\tt (x+3)^2=-4(y-3)}`

Explanation:

Definition:

A parabola is a U-shaped curve that is defined as the set of all points that are equidistant to a point called the focus and a line called the directrix.

Parabolas are often used to model the paths of projectiles, sound waves, and light rays.

For the question:

Given:

Vertex=(h,k)=(-3,3)

Focus=(-3,2)

let's find p.

Since P is the distance between vertex and focus.

We can use distance formula:

`\tt p=√((x_2-x-1)^2+(y_2-y_1)^2)`

`\tt P=√((-3-(-3))^2+(2-3)^2)`

`\tt p=√(1^2)`

p=1

therefore, p=1

length of latus rectum= 4p=4*1=1

Axis: Negative y-axis

We have, Equation of the hyperbola for Negative y-axis is in standard form is :

`\boxed{\boxed{\tt (x-h)^2=-4p(y-k)}}`

substituting value of (h,k) and p.

`\tt (x-(-3))^2=-4*1(y-3)`

`\bold{\tt (x+3)^2=-4(y-3)}`

Which is a required standard form of equation of the parabola.