To determine the intercepts of the equation
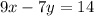 , we need to find the points where the equation intersects the
, we need to find the points where the equation intersects the
 -axis and the
-axis and the
 -axis.
-axis.
To find the
 -intercept, we set
-intercept, we set
 to zero and solve for
to zero and solve for
 .
.
When y is zero, the equation becomes:

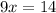
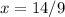
Therefore, the
 -intercept is
-intercept is
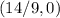 .
.
To find the
 -intercept, we set
-intercept, we set
 to zero and solve for
to zero and solve for
 .
.
When
 is zero, the equation becomes:
is zero, the equation becomes:


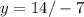
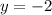
Therefore, the
 -intercept is
-intercept is
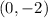 .
.
In summary, the intercepts of the equation
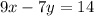 are
are
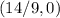 for the
for the
 -intercept and
-intercept and
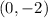 for the
for the
 -intercept. These points represent where the equation crosses the
-intercept. These points represent where the equation crosses the
 -axis and the
-axis and the
 -axis, respectively.
-axis, respectively.