Question

A football is thrown at an angle of 30. ° above the horizontal. The magnitude of the horizontal

component of the ball’s initial velocity is 13. 0 meters per second. The magnitude of the vertical

component of the ball’s initial velocity is 7. 5 meters per second. [Neglect friction. ]


The football is caught at the same height from which it is thrown. Calculate the total time the football

was in the air. [Show all work, including the equation and substitution with units. ]

Answer 1

Given:

• Horizontal component of initial velocity:
  `$v_x = 13.0\text{ m/s}$`

• Vertical component of initial velocity:
  `$v_y = 7.5\text{ m/s}$`

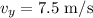
• Angle of launch:
  `$\theta = 30^\circ$`

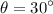
• Acceleration due to gravity:
  `$g = 9.8\text{ m/s}^2$`

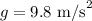
Required:

• Total time the football was in the air

Solution:

The football's vertical velocity at the highest point in its trajectory is zero. Therefore, the time it takes the football to reach the highest point is:

`(v_y)/(g) = (7.5)/(9.8) = 0.77\text{ s}`

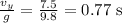
The total time the football is in the air is twice the time it takes to reach the highest point, so the total time is:

`2 * 0.77 = \boxed{1.54\text{ s}}`

Step-by-step explanation:

The time it takes the football to reach the highest point is equal to the vertical velocity divided by the acceleration due to gravity. The total time the football is in the air is twice this time, because the football has to travel up to the highest point and then back down to the ground.