Question

I need help w part c. a and b werent a problem for me, but c i keep getting 0 in denominator

Answer 1

Explanation:

the answer is A

Answer 2

A) Average rate of change = -2/17

Instantaneous rate of change: Yes, 3 times.

B) y = -3x + 17/2

C) Limit x → -1: DNE

Limit x → 3 ≈ -2

Explanation:

Part A

To calculate the average rate of change of function f over the interval [a, b], we can use the formula:

`\textsf{Average rate of change} = (f(b)-f(a))/(b-a)`

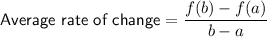
The given interval is [-2.5, 6], so a = -2.5 and b = 6.

From observation of the graph, f(-2.5) ≈ 5 and f(6) ≈ 4. Therefore:

`\begin{aligned}\textsf{Average rate of change} &= (f(6)-f(-2.5))/(6-(-2.5))\\\\&= (4-5)/(6+2.5)\\\\&= (-1)/(8.5)\\\\&=-(2)/(17)\end{aligned}`

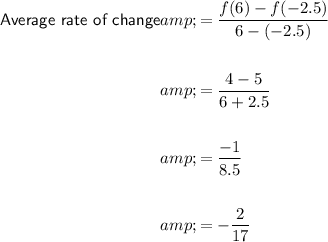
Therefore, the average rate of change of f over the interval [-2.5, 6] is approximately -2/17.

The instantaneous rate of change represents the rate of change at a specific point or instant, while the average rate of change represents the overall rate of change over an interval.

The derivative of a function represents the rate of change of the function at each point, so by examining the graph of f', we can determine the instantaneous rate of change of the original function f at any given point.

The average rate of change of f over the interval [-2.5, 6] is -2/17, which is approximately -0.12 (2 d.p.). From observation of the graph of f', there are three instances where f' ≈ -0.12. Therefore, the instantaneous rate of change of f is equivalent to the average rate of change of f over [-2.5, 6] for a total of 3 times in the given interval.

`\hrulefill`

Part B

The derivative of function f at the point x = 2 is the slope of the tangent line at x = 2 for the graph of f.

From observation of graph f', f'(2) ≈ -3.

Therefore, the estimated slope of the tangent line is -3.

From observation of graph f, f(2) ≈ 2.5.

To estimate the equation of a tangent line at x = 2 for the graph of f, substitute the found slope m = -3 and point (2, 2.5) into the point-slope formula of a linear equation:

`\begin{aligned}y-y_1&=m(x-x_1)\\\\\implies y-2.5&=-3(x-2)\\y-2.5&=-3x+6\\y&=-3x+(17)/(2)\end{aligned}`

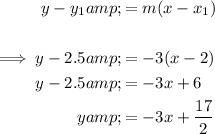
Therefore, the equation that represents the estimated tangent line at x = 2 based on the given graph of f is:

`\boxed{y=-3x+(17)/(2)}`

`\hrulefill`

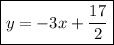
Part C

The given limits are in the form of the alternative form of the derivative formula of a function f at x = a:

`\displaystyle f'(a)=\lim_(x \to a) (f(x)-f(a))/(x-a)`

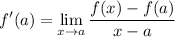
This formula represents the limit of the difference quotient as x approaches a. The difference quotient measures the rate of change of the function f at the point a and is defined as the slope of the tangent line to the graph of f at that point.

By taking the limit as x approaches a, we obtain the exact value of the derivative of f at the point a, represented as f'(a).

From the graph of f', we can see that f'(-1) does not exist. Therefore:

`f'(-1)=\displaystyle \lim_(x \to -1) (f(x)-f(-1))/(x-(-1)) = \text{DNE}`

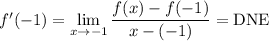
From the graph of f', we can see that f'(3) ≈ -2. Therefore:

`f'(3)=\displaystyle \lim_(x \to 3) (f(x)-f(3))/(x-(3))\approx -2`

`\hrulefill`

Additional information

Note that the equations of f and f' are:

`f(x)=3 \sin|x+1|+2`

`f'(x)=(3(x+1)\cos |x+1|)/(\left|x+1\right|)`

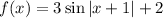
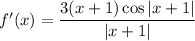
The exact average rate of change is -0.12017943...

The exact equation of the tangent line at x = 2 is y = -2.970x + 8.363 (where the coefficients are rounded to 3 decimal places).

The exact value of f'(3) = -1.96093086...

As you can see, these values are very close to the estimates we have calculated.