Question

I NEED HELP WITH THIS ASAP!

Answer 1

The LCM is:

`12x^(2) y^(2) z`

Explanation:

To find the least common multiple (LCM) of 4x^2y and 12xy^2z, we need to determine the highest power of each variable that appears in either expression.

Let's break down the given expressions into their prime factors:

`4x^(2) y=2^(2)*x^(2) *y\\12xy^(2) z=2^(2) *3*x*y^(2) *z`

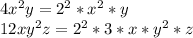
Now, we can identify the highest power of each prime factor:

2: Appears with a power of 2 in both expressions.

3: Appears with a power of 1 in the second expression only.

x: Appears with a power of 2 in the first expression only.

y: Appears with a power of 2 in the second expression only.

z: Appears with a power of 1 in the second expression only.

To find the LCM, we take the highest power of each prime factor:

LCM =
`2^(2) *3*x^(2) *y^(2) *z=12x^(2) y^(2) z`

Therefore, the LCM of 4x^2y and 12xy^2z is 12x^2y^2z.

Hope it helps!