Question

(Word Problem) (100 Points)

What Does it Mean when it Says, "Holes in the Graph".
Furthermore, How Does One Find Such "Holes"
Can Someone Please Explain?
Original Question: Name the coordinates of any holes in the graph of the function?
I am Just Looking for an Explanation of What is, & How Does One Find These "Holes"

Answer 1

In the context of graphing a function, "holes in the graph" refer to points where the graph has a missing or undefined value, resulting in a gap or discontinuity in the graph. These holes occur when there is a common factor in both the numerator and denominator of a rational function that can be canceled out, leading to a point where the function is undefined.

To find these holes in the graph, you need to follow these steps:

1) Determine if the function is a rational function: A rational function is a function that can be expressed as the ratio of two polynomial functions.

2) Identify any common factors in the numerator and denominator: Look for any terms that can be canceled out or factored out in both the numerator and denominator of the rational function.

3) Set the common factors equal to zero: Solve the equation obtained from setting the common factors equal to zero. These values represent the x-coordinates of the potential holes in the graph.

4) Simplify the function after canceling out the common factors: Once you have determined the x-coordinates of the potential holes, substitute these values back into the simplified function to find the corresponding y-coordinates.
By following these steps, you can identify the coordinates of any holes in the graph of a rational function. These holes represent points where the function is undefined, resulting in gaps or discontinuities in the graph.

Answer 2

Explanation:

A hole in the graph is a point in the graph that does not exist because of a restriction in the domain.

Here is an example.

Think of the equation y = x + 5.

The graph of this equation is a straight line with slope 1 and y-intercept 5.

There is no restriction on the domain. The domain is the entire set of real numbers, and the range is also the entire set of real numbers. Every point on the line is part of this equation. There are no "holes".

Now take that equation, and modify it by multiplying both the numerator and denominator by x + 2.

You now have the equation:

`y = ((x + 5)(x + 2))/(x + 2)`

You could have this equation given to you as

`y = (x^2 + 7x + 10)/(x + 2)`,

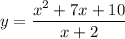but if you simplify it, you will get back to

`y = ((x + 5)(x + 2))/(x + 2)`.

Now look carefully at the equation in the form

`y = ((x + 5)(x + 2))/(x + 2)`.

You know that you can divide the numerator and denominator by the common factor x + 2, leaving the equation simplified as

y = x + 5, but there is one thing you must add to the simplified equation: it is the restriction.

y = x + 5; x ≠ -2

The graph of

`y = ((x + 5)(x + 2))/(x + 2)`

is a straight line, just like the graph of y = x + 5, but because of the binomial x + 2 in the denominator, it has the restriction on the domain of x ≠ 2, which in fact is a hole at x = -2.

The way you find holes is by looking at restrictions on the domain. Typically, you set the denominator equal to zero, and solve for x. Any value of x that causes the denominator to equal zero must be excluded from the domain causing a hole.