Question

Simplify : (13 + i)(13 - i) ​

Answer 1

Hi there!

The question asks us what the product of (13 + i)(13 - i) is.

To find that out, multiply the two complex numbers just like any two binomials - by using FOIL.

FOIL stands for:

• First
• Outside
• Inside
• Last

Multiply the first terms: 13 * 13 = 169

Multiply the outside terms: 13 * (-i) = -13i

Multiply the inside terms: i * 13 = 13i

Multiply the last terms: i*(-i) = -i²

Combine the like terms:

169 -13i + 13i - i²

169 - i²

Remember that by definition, i² = -1.

169 - (-1)

169 + 1

170

Therefore, the answer is 170.

Have a fantastic day!

Answer 2

170

Explanation:

Given expression:

(13 + i)(13 - i)

We can use the difference of the squares formula, which states that

`\tt(a + b)(a - b) = a^2 - b^2`

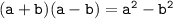
In this case, a = 13 and b = i.

Applying the formula, we have:

`\tt \: (13 + i)(13 - i) = 13^2 - i^2`

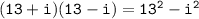
Now, we can simplify further:

`\tt 13^2 = 169`

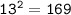
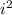`i^2` represents the square of the imaginary unit i, and it is defined as -1. Therefore:

`\tt i^2 = -1`

Substituting these values back into the equation, we get:

`\tt (13 + i)(13 - i) = 169 - (-1) = 169 + 1 = 170`

So, Therefore, the simplified expression is 170.