Question

(Please help!) Use the converse of the Pythagorean theorem to decide if the triangles are right, acute or obtuse. Then classify them

label where a, b, c is

thanks so much

Answer 1

`\mathrm{right\ triangle}`

Explanation:

`\mathrm{Take\ the\ longest\ side\ as\ }c,\mathrm{\ and\ you\ may\ assign\ any\ side\ lengths\ to\ }a\ \mathrm{and}\\b.\ \mathrm{For\ now,\ let\ }c=7,\ a=√(31)\ \mathrm{and}\ b=√(18).\\\mathrm{Now,}\\c^2=7^2=49\\a^2+b^2=(√(31))^2+(√(18))^2=31+18=49\\\mathrm{Here\ }c^2=a^2+b^2,\ \mathrm{so\ the\ pythagoras\ theorem\ is\ satisfied.\ Hence,\ the}\\\mathrm{triangle\ is\ right\ triangle.}`

Answer 2

• Right triangle

Explanation:

Pythagoras theorem states that, The square of the longest side of the triangle is equal to the sum of the other two sides of the triangle.

i.e a² + b² = c² [where c is the longest side of the triangle and a and b are the other two sides]

If a² + b² < c² then the triangle is obtuse.

If a² + b² > c² , then the triangle is acute.

If a² + b² = c² , then the triangle is right angled.

Let's solve,

From the given diagram, Longest side (c) is 7 and the other two sides (a and b) are√31 and √18 .

Using Pythagoras theorem,

»
`\sf a^2 + b^2 = c^2`

»
`\sf \sqrt{{31}^(2) }+ \sqrt{{18}^(2) } = 49`

»
`\sf 31 + 18 = 49`

»
`\sf 49 = 49`

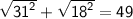
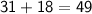
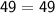
Since, a² + b² = c². Therefore The given triangle is right angled.