Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

60+4x-16=180
X=34



120+108+x=360
X=132

108+135+x=360
X=117

Answer 2

1) 34

2) 132

3) 117

Explanation:

Question 1

The given diagram shows an equilateral triangle.

Since the interior angles of an equilateral triangle are congruent, and the interior angles of a triangle sum to 180°, each interior angle of an equilateral triangle is 60°.

Angle LNM and angle MNO form a linear pair. Therefore, to find the value of x, sum the two angles to 180° and solve for x.

`\begin{aligned}m \angle LNM + \angle MNO &=180^(\circ)\\60^(\circ) + (4x-16)^(\circ) &=180^(\circ)\\60+4x-16&=180\\4x+44&=180\\4x+44-44&=180-44\\4x&=136\\4x / 4&=136 / 4\\x&=34\end{aligned}`

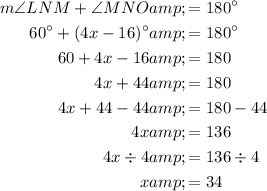
Therefore, the value of x is 34.

`\hrulefill`

Question 2

Angles around a point sum to 360°. Therefore, to find the value of x, subtract the measures of the interior angles of a regular pentagon and a regular hexagon from 360°.

To determine the interior angle of a regular polygon, we can use the formula:

`\boxed{\theta= (180^(\circ)(n-2))/(n)}`

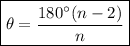
where:

• θ is the interior angle.
• n is the number of sides.

Given the number of sides of a regular pentagon is 5, substitute n = 5 into the formula:

`\begin{aligned}\textsf{Interior angle of a regular pentagon}&= (180^(\circ)(5-2))/(5)\\\\&= (180^(\circ)(3))/(5)\\\\&= (540^(\circ))/(5)\\\\&=108^(\circ)}\end{aligned}`

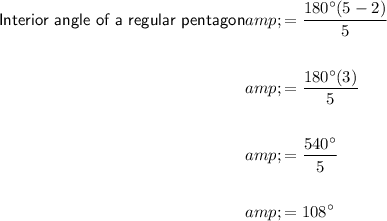
Given the number of sides of a regular hexagon is 6, substitute n = 6 into the formula:

`\begin{aligned}\textsf{Interior angle of a regular hexagon}&= (180^(\circ)(6-2))/(6)\\\\&= (180^(\circ)(4))/(6)\\\\&= (720^(\circ))/(6)\\\\&=120^(\circ)}\end{aligned}`

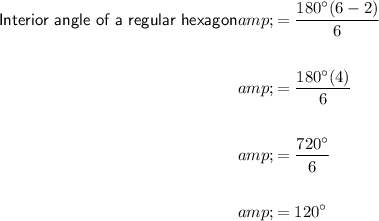
Angles around a point sum to 360°. Therefore:

`\begin{aligned} x^(\circ)+108^(\circ)+120^(\circ)&=360^(\circ)\\x+108+120&=360\\x+228&=360\\x+228-228&=360-228\\x&=132\end{aligned}`

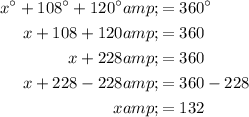
Therefore, the value of x is 132.

`\hrulefill`

Question 3

Angles around a point sum to 360°. Therefore, to find the value of x, subtract the measures of the interior angles of a regular pentagon and a regular octagon from 360°.

To determine the interior angle of a regular polygon, we can use the formula:

`\boxed{\theta= (180^(\circ)(n-2))/(n)}`

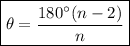
where:

• θ is the interior angle.
• n is the number of sides.

Given the number of sides of a regular pentagon is 5, substitute n = 5 into the formula:

`\begin{aligned}\textsf{Interior angle of a regular pentagon}&= (180^(\circ)(5-2))/(5)\\\\&= (180^(\circ)(3))/(5)\\\\&= (540^(\circ))/(5)\\\\&=108^(\circ)}\end{aligned}`

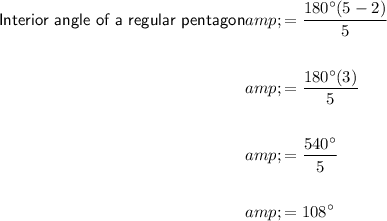
Given the number of sides of a regular octagon is 8, substitute n = 8 into the formula:

`\begin{aligned}\textsf{Interior angle of a regular octagon}&= (180^(\circ)(8-2))/(8)\\\\&= (180^(\circ)(6))/(8)\\\\&= (1080^(\circ))/(8)\\\\&=135^(\circ)}\end{aligned}`

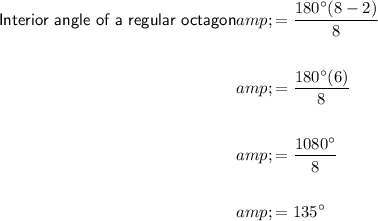
Angles around a point sum to 360°. Therefore:

`\begin{aligned} x^(\circ)+108^(\circ)+135^(\circ)&=360^(\circ)\\x+108+135&=360\\x+243&=360\\x+243-243&=360-243\\x&=117\end{aligned}`

Therefore, the value of x is 117.