Question

What is the solution to the following system of equations?

x + y = 5
{
x - y = 1

a. (-2,7)
b. (2,3)
c. (3,2)
d. (7,-2)

Answer 1

The correct answer is the ordered pairs (3,2)

Answer 2

C. (3,2)

Explanation:

Let's plug the ordered pairs one by one to determine which one of them is the solution to the system.

The system is:

`\begin{cases}\sf{x+y=5}\\\sf{x-y=1}\end{cases}`

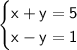
The first ordered pair is (-2,7), so I plug in -2 for x, and 7 for y :

`\begin{cases}\sf{-2+7=5}\\\sf{-2-7=1}\\\sf{5=5}\\\sf{-9=1}\end{cases}`

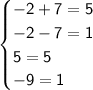
In order for an ordered pair to be a solution to a system of equations, it has to make BOTH equations true, whereas (-2,7) only satisfies one of them.

So I choose the next one - (2,3):

`\begin{cases}\sf{2+3=5}\\\sf{2-3=1}\\\sf{5=5}\\\sf{-1=1}\end{cases}`

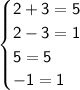
Still, one of the equations is false.

Let's choose C:

`\begin{cases}\sf{3+2=5}\\\sf{3-2=1}\\\sf{5=5}\\\sf{1=1}\end{cases}`

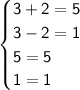
This one actually makes both equations true, so (3,2) is a solution to the system of equations.