Question

!50 POINTS! (3 SIMPLE GEOMETRY QUESTIONS)

QUESTIONS BELOW
|
|
\/

Answer 1

1) x = 20, y = -12

2) x = -5, y = 10

3) x = 15, y = 12.5

Explanation:

Question 1

In a parallelogram, opposite angles are equal.

Therefore, to find the values of x and y, equate the expressions of the angles that are opposite each other and solve for x and y.

`\begin{aligned}(7x - 11)^(\circ)&= (5x + 29)^(\circ)\\7x-11&=5x+29\\7x-11-5x&=5x+29-5x\\2x-11&=29\\2x-11+11&=29+11\\2x&=40\\2x / 2&=40 / 2\\x&=20\end{aligned}`

`\begin{aligned}(-3y+15)^(\circ)&= (-5y-9)^(\circ)\\-3y+15&=-5y-9\\-3y+15+5y&=-5y-9+5y\\2y+15&=-9\\2y+15-15&=-9-15\\2y&=-24\\2y / 2&=-24 / 2\\y&=-12\end{aligned}`

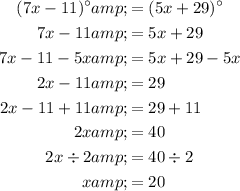
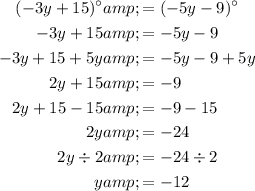
Therefore, the values of x and y are:

• x = 20
• y = -12

`\hrulefill`

Question 2

The diagonals of a parallelogram bisect each other (divide into 2 equal parts). Therefore:

`\begin{aligned}-2x+4&=-3x-1\\-2x+4+3x&=-3x-1+3x\\x+4&=-1\\x+4-4&=-1-4\\x&=-5\end{aligned}`

`\begin{aligned}5y-9&=3y+11\\5y-9-3y&=3y+11-3y\\2y-9&=11\\2y-9+9&=11+9\\2y&=20\\2y/2&=20/2\\y&=10\end{aligned}`

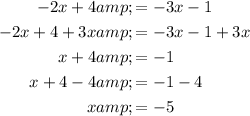
Therefore, the values of x and y are:

• x = -5
• y = 10

`\hrulefill`

Question 3

Adjacent angles in a parallelogram are supplementary (sum to 180°). Therefore:

`\begin{aligned}5x^(\circ)+45^(\circ)+60^(\circ)&=180^(\circ)\\5x^(\circ)+105^(\circ)&=180^(\circ)\\5x^(\circ)+105^(\circ)-105^(\circ)&=180^(\circ)-105^(\circ)\\5x^(\circ)&=75^(\circ)\\5x&=75\\5x / 5&=75 / 5\\x&=15\end{aligned}`

`\begin{aligned}6y^(\circ)+45^(\circ)+60^(\circ)&=180^(\circ)\\6y^(\circ)+105^(\circ)&=180^(\circ)\\6y^(\circ)+105^(\circ)-105^(\circ)&=180^(\circ)-105^(\circ)\\6y^(\circ)&=75^(\circ)\\6y&=75\\6y / 6&=75 / 6\\y&=12.5\end{aligned}`

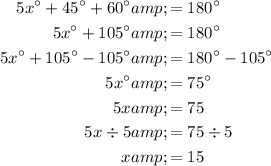
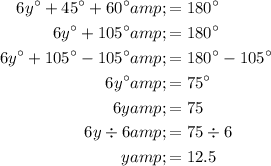
Therefore, the values of x and y are:

• x = 15
• y = 12.5