Question

Simplify ((3x - 2y)/4) - ((x - 3y)/3)

Answer 1

`\begin{aligned}(3x - 2y)/(4) - (x - 3y)/(3) &= (3(3x - 2y))/(3 * 4) - (4(x - 3y))/(4 * 3) \\&= (9x - 6y)/(12) - (4x - 12y)/(12) \\&= (9x - 6y - (4x - 12y))/(12) \\&= (9x - 4x - 6y + 12y)/(12) \\&= (5x + 6y)/(12)\end{aligned}`

Explanation:

To simplify the expression
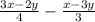`(3x - 2y)/(4) - (x - 3y)/(3)`, you need to find a common denominator for the two fractions. The least common multiple (LCM) of 4 and 3 is 12. So, you need to rewrite the fractions with the denominator of 12:

• 
  `(3(3x - 2y))/(3 * 4) - (4(x - 3y))/(4 * 3)`

Now, distribute the numerators:

• 
  `(9x - 6y)/(12) - (4x - 12y)/(12)`

Since the denominators are the same, you can combine the numerators:

• 
  `(9x - 6y - (4x - 12y))/(12)`

Now, simplify the numerator by combining like terms:

• 
  `(9x - 4x - 6y + 12y)/(12)`

• 
  `(5x + 6y)/(12)`

So, the simplified expression is
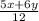
`(5x + 6y)/(12)`

_________________________________________________________